题目内容

设平面α的法向量为（1，2，-2），平面β的法向量为（-2，-4，k），若α∥β，则k=
4
4
．
分析：根据空间面面平行的判定与性质，可得两个平行平面的法向量互相平行，由此建立关于k的等式，解之即可得到实数k的值．
解答：解：∵α∥β
∴平面α、β的法向量互相平行，
由此可得
a
=（1，2，-2），
b
=（-2，-4，k），
a
∥
b

∴
1
-2
=
2
-4
=
-2
k
，解之得k=4．
故答案为：4
点评：本题给出平面α、β的法向量，在α∥β的情况下求参数k的值．着重考查了面面平行的判定与性质、向量平行与共线的计算等知识，属于基础题．
练习册系列答案
相关题目
1、设平面α的法向量为（1，2，-2），平面β的法向量为（-2，-4，k），若α∥β，则k=（　　）
设
u
=(-2，2，5)，
v
=(6，-4，4)分别是平面α，β的法向量，则平面α与β的夹角为（　　）

如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）证明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.

 

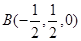【解析】解法一：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0),C(0,1,0), ,P（0,0,2）.

（1）证明：易得，于是,所以

(2) ,设平面PCD的法向量，

则,即.不防设，可得.可取平面PAC的法向量于是从而.

所以二面角A-PC-D的正弦值为.

（3）设点E的坐标为（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）证明：由，可得，又由,,故.又,所以.

(2)如图，作于点H，连接DH.由,,可得.

因此,从而为二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值为.

（3）如图，因为，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF. 故或其补角为异面直线BE与CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.

 

在四棱锥中，平面，底面为矩形，.

（Ⅰ）当时，求证：；

（Ⅱ）若边上有且只有一个点，使得，求此时二面角的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时，底面ABCD为正方形，

又因为,………………2分

又，得证。

第二问，建立空间直角坐标系，则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分

设BQ=m，则Q(1，m,0)(0《m《a》

要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得

由此知道a=2,  设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

解：(Ⅰ)当时，底面ABCD为正方形，

又因为,又………………3分

(Ⅱ) 因为AB,AD,AP两两垂直，分别以它们所在直线为X轴、Y轴、Z轴建立坐标系，如图所示，

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分

设BQ=m，则Q(1，m,0)(0《m《a》要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得由此知道a=2,

设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

 

已知直三棱柱中, , ， 是和的交点, 若.

（1）求的长；  （2）求点到平面的距离；

（3）求二面角的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中，利用ACCA为正方形, AC=3

第二问中，利用面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD=，第三问中，利用三垂线定理作二面角的平面角，然后利用直角三角形求解得到其正弦值为

解法一: (1)连AC交AC于E, 易证ACCA为正方形, AC=3 ……………  5分

(2)在面BBCC内作CDBC, 则CD就是点C平面ABC的距离CD= … 8分

(3) 易得AC面ACB, 过E作EHAB于H, 连HC, 则HCAB

CHE为二面角C－AB－C的平面角. ………  9分

sinCHE=二面角C－AB－C的平面角的正弦大小为 ……… 12分

解法二: (1)分别以直线CB、CC、CA为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

=(2, －, －), =(0, －3, －h)  ……… 4分

·=0,  h=3

(2)设平面ABC得法向量=(a, b, c),则可求得=(3, 4, 0) (令a=3)

点A到平面ABC的距离为H=||=……… 8分

(3) 设平面ABC的法向量为=(x, y, z),则可求得=(0, 1, 1) (令z=1)

二面角C－AB－C的大小满足cos== ………  11分

二面角C－AB－C的平面角的正弦大小为

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网