题目内容
若椭圆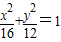 上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )
上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
【答案】分析:由椭圆的定义结合题意可得三角形的三边,由勾股定理可得结论.
解答:解:由椭圆的定义可得:|PF1|+|PF2|=2a=8,
又知|PF1|-|PF2|=2,两式联立可得
|PF1|=5,|PF2|=3,又|F1F2|=2c=4
故满足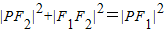 ,
,
故△PF1F2是直角三角形.
故选B
点评:本题为三角形形状的判断,由椭圆的定义解出三角形的三边是解决问题的关键,属中档题.
解答:解:由椭圆的定义可得:|PF1|+|PF2|=2a=8,
又知|PF1|-|PF2|=2,两式联立可得
|PF1|=5,|PF2|=3,又|F1F2|=2c=4
故满足
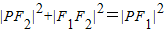 ,
,故△PF1F2是直角三角形.
故选B
点评:本题为三角形形状的判断,由椭圆的定义解出三角形的三边是解决问题的关键,属中档题.

练习册系列答案
相关题目
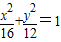 上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )
上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )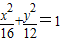 上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )
上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )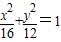 上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )
上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )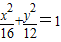 上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )
上一点P到两焦点F1、F2的距离之差为2,则△PF1F2是( )