题目内容
已知命题P：函数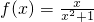
在区间（a，2a+1）上是单调递增函数；命题Q：不等式（a-2）x2+2（a-2）x-4＜0对任意实数x恒成立．若P∨Q是真命题，求实数a的取值范围．
解：若P是真，求导函数f′（x）=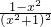
，令f′（x）＞0可得-1＜x＜1
∵函数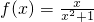在区间（a，2a+1）上是单调递增函数
∴
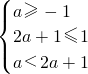，∴-1＜a≤0
若Q是真，可得a=2或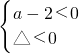
得：-2＜a≤2，
∵P∨Q是真命题，∴P真Q假或P假Q真或P真Q真
若P真Q假，则
，∴a∈∅；
若P假Q真，则
，∴-2＜a≤-1或0＜a≤2
若P真Q真，则
，∴-1＜a≤0
∴由P∨Q是真命题可得a∈（-2，2]．
分析：先求出P，Q为真时，参数的取值范围，再将P∨Q是真命题，转化为P真Q假或P假Q真或P真Q真，即可求得实数a的取值范围．
点评：解决本题的灵魂在于“转化”，将P∨Q是真命题，转化为P真Q假或P假Q真或P真Q真．
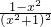，令f′（x）＞0可得-1＜x＜1∵函数
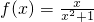在区间（a，2a+1）上是单调递增函数∴
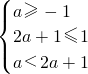，∴-1＜a≤0若Q是真，可得a=2或
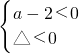得：-2＜a≤2，∵P∨Q是真命题，∴P真Q假或P假Q真或P真Q真
若P真Q假，则
，∴a∈∅；若P假Q真，则
，∴-2＜a≤-1或0＜a≤2若P真Q真，则
，∴-1＜a≤0∴由P∨Q是真命题可得a∈（-2，2]．
分析：先求出P，Q为真时，参数的取值范围，再将P∨Q是真命题，转化为P真Q假或P假Q真或P真Q真，即可求得实数a的取值范围．
点评：解决本题的灵魂在于“转化”，将P∨Q是真命题，转化为P真Q假或P假Q真或P真Q真．
练习册系列答案
相关题目