题目内容
在数列{an}中,若a1=a(a>2),且an+ 1=(1)an>2;
(2)an+ 1<an
答案:
解析:
解析:
| (1)①当n=1时,a1=a>2,命题成立.
②假设当n=k(k∈N*)时,命题成立, 即ak>2,则ak-1>0且 于是 > 这就是说,当n=k+1时,原命题也成立. 根据①和②可知,对一切n∈N*,都有an>2. (2) ∵ an>2 ∴ 即an+1<an |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
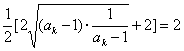
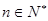 ),则该数列的通项an= 。
),则该数列的通项an= 。