题目内容
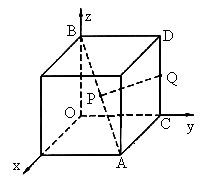
如图所示,正方体边长为
1,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.(1)
当点P为对角线AB中点,点Q在棱CD上运动时,求|PQ|的最小值;(2)
当点Q为棱CD的中点,点P在对角线AB上运动时,求|PQ|的最小值.
答案:略
解析:
解析:
|
解: (1)依题意P(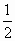 , ,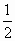 , ,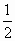 ).设Q(0,1,z),则 ).设Q(0,1,z),则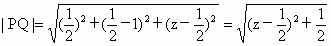 ,所以当 ,所以当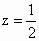 时 时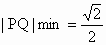 ,此时Q(0,1, ,此时Q(0,1,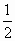 )恰为CD中点; )恰为CD中点;
(2) 依题意Q(0,1,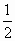 ),设P(x,x,z)则 ),设P(x,x,z)则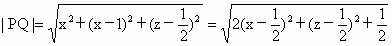 所以当 所以当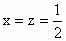 时, 时,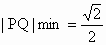 ,此时P点坐标为P( ,此时P点坐标为P(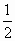 , ,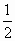 , ,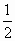 ),恰为AB的中点. ),恰为AB的中点. |

练习册系列答案
相关题目
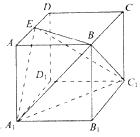
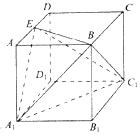
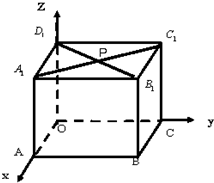 (1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.
(1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.