题目内容
设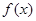 是定义在
是定义在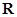 上的奇函数,且当
上的奇函数,且当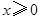 时,
时,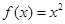 ,若对任意的
,若对任意的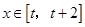 ,不等式
,不等式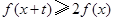 恒成立,则实数
恒成立,则实数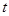 的取值范围是( )
的取值范围是( )
A.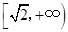 B.
B.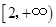
C.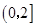 D.
D.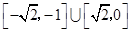
【答案】
A
【解析】
试题分析:当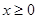 ,
,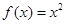 ,又函数是奇函数,所以当
,又函数是奇函数,所以当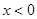 时,
时,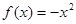 ,所以
,所以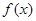 是R上的单调递增函数,且满足
是R上的单调递增函数,且满足 ,又因为不等式
,又因为不等式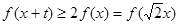 在
在 恒成立,
恒成立,
所以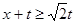 在
在 恒成立,即
恒成立,即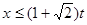 在
在 恒成立,所以
恒成立,所以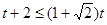 ,解得
,解得
 .选A.
.选A.
考点:函数恒成立问题;函数奇偶性的性质.
点评:本题考查了函数恒成立问题及函数的奇偶性,难度适中,关键是掌握函数的单调性与奇偶性.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, ,若对任意
,若对任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 . 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ( )
( ) B.
B.  C.
C.
 D.
D. 
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .若对任意的
.若对任意的 ,
,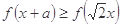 恒成立,则实数
恒成立,则实数 的取值范围是(
)
的取值范围是(
) B.
B. C.
C. D.
D.