题目内容
某牛奶生产线上每隔30分钟抽取一袋进行检验,则该抽样方法为①;从某中学的30名数学爱好者中抽取3人了解学习负担情况,则该抽样方法为②.那么( )
| A.①是系统抽样,②是简单随机抽样 |
| B.①是分层抽样,②是简单随机抽样 |
| C.①是系统抽样,②是分层抽样 |
| D.①是分层抽样,②是系统抽样 |
A
解析考点:系统抽样方法.
分析:根据系统抽样方法是等距抽样,简单随机抽样对个体之间差别不大,且总体和样本容量较小时采用,从而可得结论.
解:∵牛奶生产线上每隔30分钟抽取一袋进行检验,是等距的
∴①为系统抽样
某中学的30名数学爱好者中抽取3人了解学习负担情况
个体之间差别不大,且总体和样本容量较小,
∴②为简单随机抽样法
故答案为:A

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
某单位共有老、中、青职工430人,其中青年职工160人, 中年职工人数是老年职工人数的2倍. 为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 ( )
中年职工人数是老年职工人数的2倍. 为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 ( )
| A.9 | B.18 | C.27 | D.36 |
下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
| B.线性回归方程对应的直线=x+至少经过点其样本数据(x1,y1),(x2,y2),…,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中,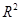 为0.98的模型比 为0.98的模型比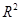 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |
如图,是某篮球运动员在一个赛季的30场比赛中得分的茎叶图,则得分的中位数与众数分别为( )
| A. 3与3 | B.23与3 | C.3与23 | D.23与23 |
在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连 续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A.甲地:总体均值为3,中位数为4 | B.乙地:总体均值为1,总体方差大于0 |
| C.丙地:中位数为2,众数为3 | D.丁地:总体均值为2,总体方差为3 |
某高中共有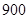 人,其中高一年级
人,其中高一年级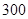 人,高二年级
人,高二年级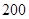 人,高三年级
人,高三年级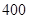 人,现采用分层抽样抽取容量为
人,现采用分层抽样抽取容量为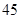 的样本,那么高一、高二、高三各年级抽取的人数分别为
的样本,那么高一、高二、高三各年级抽取的人数分别为
A.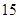 , ,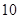 , ,  | B.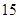 , ,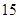 , ,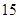 | C.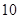 , , 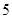 , , | D.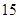 , , 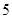 , ,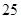 |
甲、乙两名射击运动员在某次测试中各射击20次,两人的测试成绩如下表
| 甲的成绩 | | 乙的成绩 | ||||||||
| 环数 | 7 | 8 | 9 | 10 | | 环数 | 7 | 8 | 9 | 10 |
| 频数 | 6 | 4 | 4 | 6 | | 频数 | 4 | 6 | 6 | 4 |
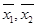 分别表示甲、乙两名运
分别表示甲、乙两名运动员这次测试中成绩的平均数,则有
A.
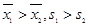 B.
B.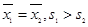 C.
C.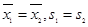 D.
D.
为了了解全校240名高一学生的身高情况,从中抽取40名学生进行测量,下列说法正确的是( )
| A.总体是240 | B.个体是每一个学生 |
| C.样本是40名学生 | D.样本容量是40 |
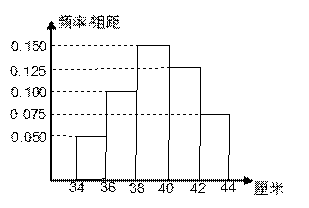
 长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是
长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是