题目内容
已知二次函数的图象经过原点及点(-
,
),且图象与x轴的负半轴的交点到原点的距离为1,则该二次函数的解析式为 .
| 1 |
| 2 |
| 1 |
| 4 |
分析:设二次函数的解析式为:y=ax2+bx+c,a≠0,由题意可得函数图象过原点和点(-
,
),以及(-1,0),可得关于a、b、c的方程组,解方程组可得解析式.
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:设二次函数的解析式为:y=ax2+bx+c,a≠0,
由二次函数的图象经过原点及点(-
,
)可得
,
化简可得c=0,a-2b=1,①
又函数图象与x轴的负半轴的交点到原点的距离为1,
∴函数图象过点(-1,0),∴0=a-b ②
由①②解得a=b=-1
∴所求函数的解析式为:y=-x2-x
故答案为:y=-x2-x
由二次函数的图象经过原点及点(-
| 1 |
| 2 |
| 1 |
| 4 |
|
化简可得c=0,a-2b=1,①
又函数图象与x轴的负半轴的交点到原点的距离为1,
∴函数图象过点(-1,0),∴0=a-b ②
由①②解得a=b=-1
∴所求函数的解析式为:y=-x2-x
故答案为:y=-x2-x
点评:本题考查函数解析式的求解,涉及待定系数法以及方程组的求解,属基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.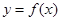 的图象经过原点,且
的图象经过原点,且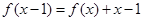 。
。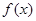 的表达式.
的表达式.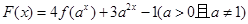 ,当
,当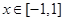 时,
时,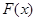 有最大值14,试求
有最大值14,试求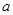 的值.
的值. 的图象经过点
的图象经过点 ,
, 是偶函数,函数
是偶函数,函数 的图象与直线
的图象与直线 相切,且切点位于第一象限
相切,且切点位于第一象限 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 有三个不同的实数解,求实数k的值
有三个不同的实数解,求实数k的值