题目内容
对于平面内的命题:“△ABC内接于圆⊙O,圆O的半径为R,且O点在△ABC内,连结AO,BO,CO并延长分别交对边于A1,B1,C1,则AA1+BB1+CC1≥![]() ”
”
证明如下:![]()
即:![]() ,即
,即![]()
由柯西不等式,得![]()
∴AA1+BB1+CC1≥![]()
将平面问题推广到空间,就得到命题“四面体ABCD内接于半径为R的球O内,球心O在该四面体内,连结AO,BO,CO,DO并延长分别与对面交于A1,B1,C1,D1,则________”
答案:
解析:
解析:
|
AA1+BB1+CC1+CC1≥ |

练习册系列答案
相关题目
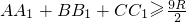 ”.
”.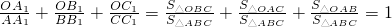 ,
,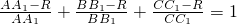 ,即
,即 ,
,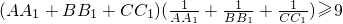 .∴
.∴ ”.
”. ,
, ,即
,即 ,
, .∴
.∴ .
.