Question

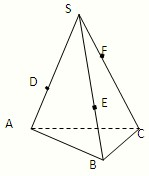
如图，一个盛满水的三棱锥容器，三条侧棱上各有一个小洞D，E，F，且知道SD：DA=SE：EB=CF：FS=2：1，若仍用这个容器盛水，则最多可盛原来水的

23

27

．

Answer 1

分析：由实际情况可以得到，当DEF面与地面平行时，此时盛水最多，由此知，可求出不规则几何体DEFABC的体积，此体积所点三棱锥S-ABC的比即为所求的正确答案．

解答：解：如右图所示，过DE作与底面ABC平行的截面DEM，则M为SC的中点，F为SM的中点．过F作与底面ABC平行的截面FNP，则N，P分别为SD，SE的中点．
设三棱锥S-ABC的体积为V，高为H，S-DEM的体积为V₁，高为h，则

h

H

=

2

3

，

V1

V

=(

2

3

)3=

8

27

．
三棱锥F-DEM的体积与三棱锥S-DEM的体积的比是1：2（高的比），
∴三棱锥F-DEM的体积

4V

27

．三棱台DEM-ABC的体积=V-V₁=

19V

27

，
∴最多可盛水的容积=

4V

27

+

19V

27

=

23V

27

．
故最多所盛水的体积是原来的

23

27

．
故答案为：

23

27

．

点评：本题考查棱柱，棱锥，棱台的体积的求法，解题的关键是掌握相应的体积公式及几何体的结构，将求不规则几何体的体积变为求几个规则的几何体的体积，分割法求体积是求不规则几何体体积时常用的技巧