题目内容
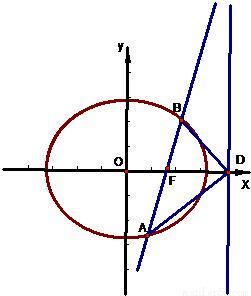
 如图,椭圆Q:
如图,椭圆Q:![]() (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(1) 求点P的轨迹H的方程
(2) 在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q£![]() ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
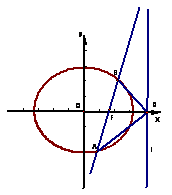
 解:如图,(1)设椭圆Q:
解:如图,(1)设椭圆Q:![]() (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
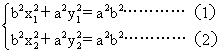
1°当AB不垂直x轴时,x1¹x2,
由(1)-(2)得
b2(x1-x2)2x+a2(y1-y2)2y=0
![]()
b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为,椭圆Q右准线l方程是x=![]() ,原点距l的距离为
,原点距l的距离为![]() ,
,
由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£![]() )
)
则![]() =
=![]() =2sin(
=2sin(![]() )
)
当q=![]() 时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
设椭圆Q:![]() 上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
S=![]() |y1|+
|y1|+![]() |y2|=
|y2|=![]() |y1-y2|
|y1-y2|
设直线m的方程为x=ky+1,代入![]() 中,得(2+k2)y2+2ky-1=0
中,得(2+k2)y2+2ky-1=0
由韦达定理得y1+y2=![]() ,y1y2=
,y1y2=![]() ,
,
4S2=(y1-y2)2=(y1+y2)2-4 y1y2=![]()
![]()
令t=k2+1³1,得4S2=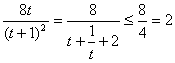 ,当t=1,k=0时取等号。
,当t=1,k=0时取等号。
因此,当直线m绕点F转到垂直x轴位置时,三角形ABD的面积最大。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目


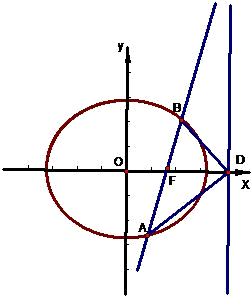 如图,椭圆Q:
如图,椭圆Q: (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点. ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?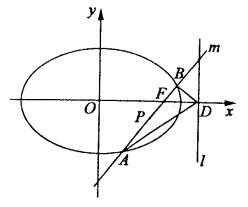
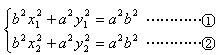 ).
).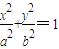 (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.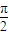 ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?