题目内容
(本小题满分12分)已知直线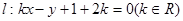
(1)证明:直线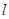 过定点;
过定点;
(2)若直线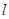 交
交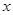 轴负半轴于
轴负半轴于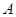 ,交
,交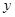 轴正半轴于
轴正半轴于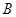 ,
,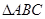 的面积为
的面积为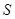 ,求
,求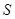 的最小值并求此时直线
的最小值并求此时直线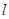 的方程。
的方程。
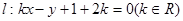
(1)证明:直线
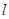 过定点;
过定点;(2)若直线
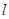 交
交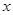 轴负半轴于
轴负半轴于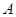 ,交
,交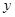 轴正半轴于
轴正半轴于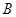 ,
,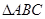 的面积为
的面积为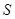 ,求
,求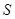 的最小值并求此时直线
的最小值并求此时直线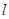 的方程。
的方程。(1)见解析;(2)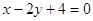 。
。
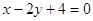 。
。本试题主要是考查了直线的方程与三角形面积公式的运用。
(1)因为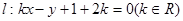 ,那么化为关于k的表达式,无论k取何值,都成立,因此可得结论。
,那么化为关于k的表达式,无论k取何值,都成立,因此可得结论。
(2)由 的方程得,
的方程得,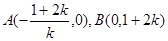 ,由题意有
,由题意有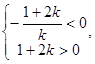
解得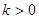 ,因为
,因为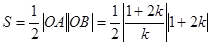 ,由不等式求得最值。
,由不等式求得最值。
解:(1)直线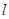 的方程可化为
的方程可化为 令
令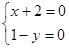 ,解得
,解得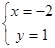 ,
,
所以,无论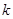 取何值,直线总经过定点
取何值,直线总经过定点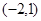 --------------------5分
--------------------5分
(2)由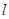 的方程得,
的方程得,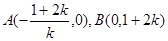 ,由题意有
,由题意有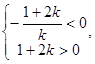
解得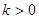 ,因为
,因为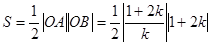 ----------9分
----------9分
即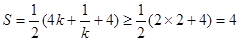 。
。
当且仅当 即
即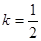 时,
时,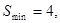
此时直线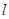 的方程为
的方程为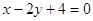 。-----------------------12分
。-----------------------12分
(1)因为
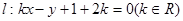 ,那么化为关于k的表达式,无论k取何值,都成立,因此可得结论。
,那么化为关于k的表达式,无论k取何值,都成立,因此可得结论。(2)由
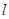 的方程得,
的方程得,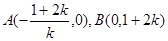 ,由题意有
,由题意有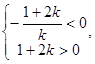
解得
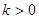 ,因为
,因为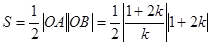 ,由不等式求得最值。
,由不等式求得最值。解:(1)直线
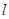 的方程可化为
的方程可化为 令
令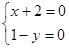 ,解得
,解得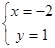 ,
,所以,无论
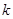 取何值,直线总经过定点
取何值,直线总经过定点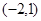 --------------------5分
--------------------5分(2)由
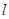 的方程得,
的方程得,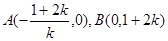 ,由题意有
,由题意有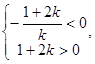
解得
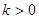 ,因为
,因为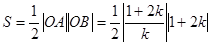 ----------9分
----------9分即
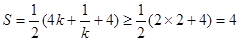 。
。当且仅当
 即
即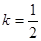 时,
时,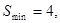
此时直线
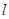 的方程为
的方程为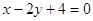 。-----------------------12分
。-----------------------12分
练习册系列答案
相关题目
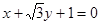 垂直的直线的倾斜角为 ( )
垂直的直线的倾斜角为 ( )



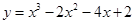 在点
在点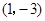 处的切线方程是 .
处的切线方程是 . 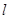 的方程为
的方程为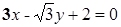 ,则与
,则与 和
和 的直线的斜率等于
的直线的斜率等于 ,那么
,那么 的值为( )
的值为( )

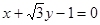 的倾斜角是
的倾斜角是



 的斜率为( )
的斜率为( )


