题目内容
.已知函数![]() ,其中
,其中![]() 为大于零的常数.
为大于零的常数.
(Ⅰ)当a=1时,求函数![]() 的单调区间,
的单调区间,
(Ⅱ)求函数![]() 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;
(Ⅲ)求证:对于任意的![]() n>1时,都有
n>1时,都有![]() >
>![]() 成立.
成立.
答案: ![]() (Ⅰ)当a=1时,
(Ⅰ)当a=1时,![]() .
.
当x>1时,![]() ;当0<x<1时,
;当0<x<1时,![]() .∴f(x)的增区间为(1,+∞),减区间为(0,1).
.∴f(x)的增区间为(1,+∞),减区间为(0,1).
(Ⅱ)当![]() 时,
时,![]() 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时![]() 在[1,2]上为增函数
在[1,2]上为增函数![]() .
.
当![]()
![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
这时![]() 在[1,2]上为减函数
在[1,2]上为减函数![]()
当![]() 时, 令
时, 令![]()
又![]()
![]()
![]()
综上,![]() 在[1,2]上的最小值为①当
在[1,2]上的最小值为①当![]()
②当![]() 时,
时,![]() ③当
③当![]()
(Ⅲ)由(Ⅰ)知函数![]() 上为增函数,
上为增函数,
当![]()
![]() 即
即![]() 恒成立
恒成立
![]()
![]()
![]()
![]() 恒成立.
恒成立.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
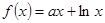 ,其中
,其中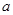 为常数,设
为常数,设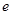 为自然对数的底数.
为自然对数的底数.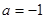 时,求
时,求 的最大值;
的最大值; 上的最大值为
上的最大值为 ,求
,求 ,其中
,其中 为正常数.
为正常数. 在
在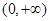 上的最大值;
上的最大值; 满足:
满足: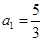 ,
, ,
,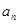 ;
; ,
, ;
; .
. (其中
(其中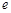 为自然对数的底数),
为自然对数的底数), .
. ,
,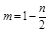 ,求
,求 在
在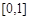 上的最大值;
上的最大值;  时方程
时方程 在
在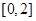 上恰有两个相异实根,求
上恰有两个相异实根,求 的取值范围;
的取值范围;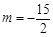 ,
, ,求使
,求使 的图象恒在
的图象恒在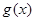 图象上方的最大正整数
图象上方的最大正整数 .
. ]
]