题目内容
2008年奥运会在北京举行,奥运会期间需从8名志愿者中选出英语、俄语和日语的志愿者各一名组成一服务小组,已知8名志愿者中A1,A2,A3,A4会英语,B1,B2,B3会俄语,只有C会日语.
(1)求B1被选中的概率;
(2)求B1和A1不全被选中的概率.
(1)求B1被选中的概率;
(2)求B1和A1不全被选中的概率.
分析:(1)根据题意,会俄语的有B1,B2,B3,共三人,而从中选出一人,由等可能事件的概率公式计算可得答案;
(2)首先计算A1被选中的概率,结合(1)的结论由相互独立事件概率的乘法公式可得B1、A1全被选中的概率,由对立事件的概率性质计算可得答案.
(2)首先计算A1被选中的概率,结合(1)的结论由相互独立事件概率的乘法公式可得B1、A1全被选中的概率,由对立事件的概率性质计算可得答案.
解答:解:(1)根据题意,会俄语的有B1,B2,B3,共三人,
要从中选出一人,则B1被选中的概率P1=
;
(2)根据题意,A1,A2,A3,A4四人会英语,则A1被选中的概率P2=
,
则B1、A1全被选中的概率为P3=
×
=
,
∴B1、A1不全被选中的概率为P4=1-
=
.
要从中选出一人,则B1被选中的概率P1=
| 1 |
| 3 |
(2)根据题意,A1,A2,A3,A4四人会英语,则A1被选中的概率P2=
| 1 |
| 4 |
则B1、A1全被选中的概率为P3=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
∴B1、A1不全被选中的概率为P4=1-
| 1 |
| 12 |
| 11 |
| 12 |
点评:本题考查等可能事件的概率的计算,注意正确理解“不全被选中”的含义,并准确计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
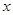 个月,顾客对某种奥运商品的需求总量
个月,顾客对某种奥运商品的需求总量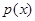 件与月份
件与月份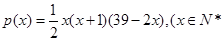 且
且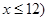 ,该商品的进价
,该商品的进价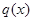 元与月份
元与月份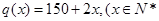 且
且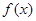 件与月份
件与月份