题目内容
在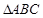 中,已知
中,已知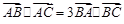 .
.
(1)求证: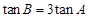 ;
;
(2)若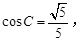 求角A的大小.
求角A的大小.
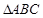 中,已知
中,已知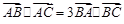 .
.(1)求证:
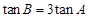 ;
; (2)若
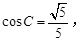 求角A的大小.
求角A的大小.(1)证明见解析;(2)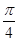 .
.
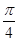 .
.试题分析:(1)已知的向量的数量积,要证明的是角的关系,故我们首先运用数量积定义把已知转化为三角形的边角关系,由已知可得
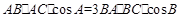 ,即
,即 ,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有
,考虑到求证式只是角的关系,因此我们再应用正弦定理把式子中边的关系转化为角的关系,即有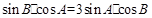 ,而这时两边同除以
,而这时两边同除以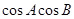 即得待证式(要说明
即得待证式(要说明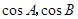 均不为零).(2)要求解
均不为零).(2)要求解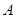 的大小,一般是求出这个角的某个三角函数值,本题应该求
的大小,一般是求出这个角的某个三角函数值,本题应该求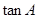 ,因为(1)中有
,因为(1)中有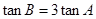 可利用,思路是
可利用,思路是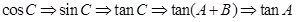 .
.试题解析:(1)∵
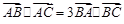 ,∴
,∴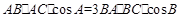 ,
,即
 . 2分
. 2分由正弦定理,得
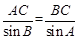 ,∴
,∴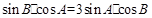 . 4分
. 4分又∵
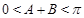 ,∴
,∴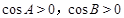 .∴
.∴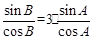 即
即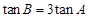 . 6分
. 6分(2)∵
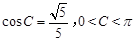 ,∴
,∴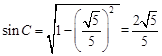 .∴
.∴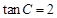 .8分
.8分∴
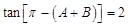 ,即
,即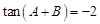 .∴
.∴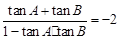 . 10分
. 10分由 (1) ,得
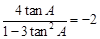 ,解得
,解得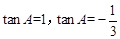 . 12分
. 12分∵
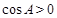 ,∴
,∴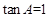 .∴
.∴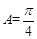 . 14分
. 14分
练习册系列答案
相关题目
 .
. 中,
中, ,求
,求 的值;
的值; 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程. 为常数).
为常数). 时,
时, 的最小值为
的最小值为 ,求a的值.
,求a的值.
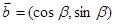 ,下列结论中正确的是( )
,下列结论中正确的是( )


 、
、 的夹角为
的夹角为
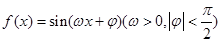 的最小正周期为
的最小正周期为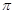 ,若其图象向右平移
,若其图象向右平移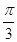 个单位后关于y轴对称,则( )
个单位后关于y轴对称,则( )



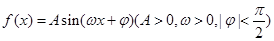 的部分图像如图示,则将
的部分图像如图示,则将 的图像向右平移
的图像向右平移 个单位后,得到的图像解析式为( )
个单位后,得到的图像解析式为( )




 为三角形ABC的一个内角,若
为三角形ABC的一个内角,若 ,则这个三角形的形状为 ( )
,则这个三角形的形状为 ( ) 的值域是 .
的值域是 .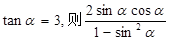 的值为( )
的值为( )