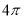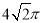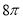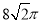题目内容
(本小题满分12分)已知幂函数 的图象经过点
的图象经过点 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)判断函数 在区间
在区间 上的单调性,并用单调性的定义证明.
上的单调性,并用单调性的定义证明.
(Ⅰ)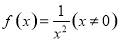 ;(Ⅱ)
;(Ⅱ)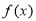 在区间
在区间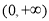 上是减函数.
上是减函数.
【解析】
试题分析:(Ⅰ)属待定系数法求函数解析式,即设出函数方程,代入点计算待定系数
(Ⅱ)利用单调性的定义证明单调性,三步:取数并规定大小,作差比较两函数大小,判断点调性
试题解析:(Ⅰ)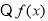 是幂函数,设
是幂函数,设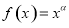 (
(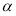 是常数)
是常数)
由题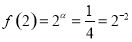 ,所以
,所以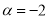
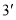
所以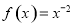 ,即
,即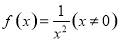
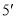
(Ⅱ)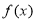 在区间
在区间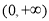 上是减函数.证明如下:
上是减函数.证明如下: 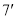
设 ,且
,且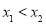 ,则
,则 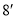
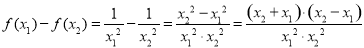
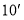
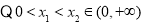
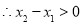 ,
,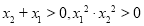
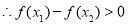 即
即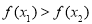
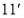
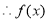 在区间
在区间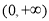 上是减函数.
上是减函数. 
考点:函数解析式的求法,单调性的定义

练习册系列答案
相关题目