题目内容
从6个高度不同的同学中选取5个同学排成一排照相,要求偶数位置的同学高于相邻两个奇数位置的同学,则可产生的照片数是( )A.60
B.72
C.84
D.96
【答案】分析:若从五人中的身高是前两名排在第二,四位有 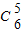 •
•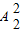 •
•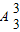 种方法.若第一高排在2号第二高排在1号,第三高排
种方法.若第一高排在2号第二高排在1号,第三高排
在4号,或第一高排在4号第二高在5号,第三高在2号,共有2×2×6种方法.把这两类的方法数相加,即得所求.
解答:解:先挑出五个有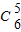 =6种 方法.
=6种 方法.
若从五人中的身高是前两名排在第二,四位有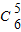 •
•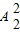 •
•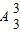 =72种方法.
=72种方法.
若第一高排在2号第二高排在1号,第三高排在4号,或第一高排在4号第二高在5号,第三高在2号,
共有2×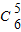 +2×
+2×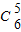 =24种方法.
=24种方法.
综上,可产生的照片数是72+24=96 种方法,
故选D.
点评:本题主要考查排列与组合及两个基本原理,排列数公式、组合数公式的应用,注意特殊元素和特殊位置,要优先考虑,
体现了分类讨论的数学思想,属于中档题.
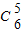 •
•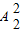 •
•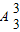 种方法.若第一高排在2号第二高排在1号,第三高排
种方法.若第一高排在2号第二高排在1号,第三高排在4号,或第一高排在4号第二高在5号,第三高在2号,共有2×2×6种方法.把这两类的方法数相加,即得所求.
解答:解:先挑出五个有
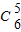 =6种 方法.
=6种 方法. 若从五人中的身高是前两名排在第二,四位有
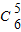 •
•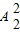 •
•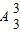 =72种方法.
=72种方法.若第一高排在2号第二高排在1号,第三高排在4号,或第一高排在4号第二高在5号,第三高在2号,
共有2×
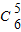 +2×
+2×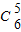 =24种方法.
=24种方法.综上,可产生的照片数是72+24=96 种方法,
故选D.
点评:本题主要考查排列与组合及两个基本原理,排列数公式、组合数公式的应用,注意特殊元素和特殊位置,要优先考虑,
体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目