题目内容
圆x2+y2-2axcosθ-2bysinθ-a2sin2θ=0在x轴上截得的弦长为
- A.
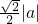
- B.
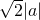
- C.2|a|
- D.4|a|
C
分析：令y=0代入圆的方程，可得关于x的二次方程，求出两个根，可得弦长的值．
解答：令y=0代入圆的方程，可得x2-2axcosθ-a2sin2θ=0，即（x-acosθ）2=a2，∴x=acosθ±a．
截x轴所得弦长为|（acosθ+a）-（acosθ-a）|=2|a|．
故选：C．
点评：本题主要考查圆的一般方程，直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，是中档题．初看无思路，边做边看，柳暗花明，是解答数学问题常用的策略．
分析：令y=0代入圆的方程，可得关于x的二次方程，求出两个根，可得弦长的值．
解答：令y=0代入圆的方程，可得x2-2axcosθ-a2sin2θ=0，即（x-acosθ）2=a2，∴x=acosθ±a．
截x轴所得弦长为|（acosθ+a）-（acosθ-a）|=2|a|．
故选：C．
点评：本题主要考查圆的一般方程，直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，是中档题．初看无思路，边做边看，柳暗花明，是解答数学问题常用的策略．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目