题目内容
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=T f(x)成立.
(1)函数f(x)= x 是否属于集合M?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明: f(x)=ax∈M;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围.
(1)f(x)=![]() (2)证明略(3)实数k的取值范围是{k|k= mπ, m∈Z}
(2)证明略(3)实数k的取值范围是{k|k= mπ, m∈Z}
解析:
【解题思路】函数f(x)是否属于集合M,要看f(x)是否满足集合M的“定义”,
[解](1)对于非零常数T,f(x+T)=x+T, Tf(x)=Tx. 因为对任意x∈R,x+T= Tx不能恒成立,所以f(x)=![]()
(2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点,
所以方程组: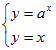 有解,消去y得ax=x,
有解,消去y得ax=x,
显然x=0不是方程ax=x的解,所以存在非零常数T,使aT=T.
于是对于f(x)=ax有![]() 故f(x)=ax∈M.
故f(x)=ax∈M.
(3)当k=0时,f(x)=0,显然f(x)=0∈M.
当k≠0时,因为f(x)=sinkx∈M,所以存在非零常数T,对任意x∈R,有
f(x+T)=T f(x)成立,即sin(kx+kT)=Tsinkx .
因为k≠0,且x∈R,所以kx∈R,kx+kT∈R,
于是sinkx ∈[-1,1],sin(kx+kT) ∈[-1,1],
故要使sin(kx+kT)=Tsinkx .成立,
只有T=![]() ,当T=1时,sin(kx+k)=sinkx 成立,则k=2mπ, m∈Z .
,当T=1时,sin(kx+k)=sinkx 成立,则k=2mπ, m∈Z .
当T=-1时,sin(kx-k)=-sinkx 成立,
即sin(kx-k+π)= sinkx 成立,
则-k+π=2mπ, m∈Z ,即k=-2(m-1) π, m∈Z .
实数k的取值范围是{k|k= mπ, m∈Z}
