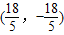题目内容
已知A(4,3),且P是双曲线x2-y2=2上一点,F2为双曲线的右焦点,则|PA|+|PF2|的最小值是 .
分析:x2-y2=2⇒
-
=1⇒实半轴a=
,半焦距c=2,从而可求F2(2,0),利用双曲线的定义|PF2|=|PF1|-2a及不等式即可求得|PA|+|PF2|的最小值.
| x2 |
| 2 |
| y2 |
| 2 |
| 2 |
解答:解:∵x2-y2=2,
∴
-
=1,
∴其实半轴a=
,半焦距c=2,
∴右焦点F2(2,0),左焦点F1(-2,0);
又A(4,3),P是双曲线x2-y2=2上一点,
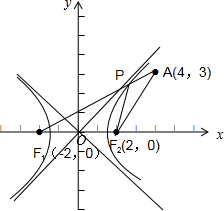
∴当点P在双曲线
-
=1右支上时,|PA|+|PF2|取得最小值,
∴|PF2|=|PF1|-2a=|PF1|-2
,
∴|PA|+|PF2|=|PA|+|PF1|-2
≥|AF1|-2
=
-2
=3
-2
.
故答案为:3
-2
.
∴
| x2 |
| 2 |
| y2 |
| 2 |
∴其实半轴a=
| 2 |
∴右焦点F2(2,0),左焦点F1(-2,0);
又A(4,3),P是双曲线x2-y2=2上一点,

∴当点P在双曲线
| x2 |
| 2 |
| y2 |
| 2 |
∴|PF2|=|PF1|-2a=|PF1|-2
| 2 |
∴|PA|+|PF2|=|PA|+|PF1|-2
| 2 |
≥|AF1|-2
| 2 |
=
| [4-(-2)]2+(3-0)2 |
| 2 |
=3
| 5 |
| 2 |
故答案为:3
| 5 |
| 2 |
点评:本题考查双曲线的简单性质,由双曲线的定义将|PF2|转化为|PF2|=|PF1|-2a是关键,考查分析与运算能力,属于中档题.

练习册系列答案
相关题目
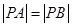 ,且点P到L的距离等于2
,且点P到L的距离等于2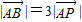 ,则P点的坐标为( )
,则P点的坐标为( )