题目内容
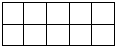
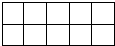
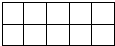
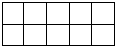
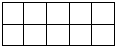10、在如图所示的10块地上选出6块种植A1、A2、…、A6等六个不同品种的蔬菜，每块种植一种不同品种蔬菜，若A1、A2、A3必须横向相邻种在一起，A4、A5横向、纵向都不能相邻种在一起，则不同的种植方案有（ ）分析：本题是一个分类和分步原理的综合应用，A1、A2、A3横向相邻种，在这三种蔬菜的排列就是1×2×3，同时排在上排与排在下排又是两种方案，比较复杂的是A4与A5的可以选择的方案．分两种情况，当A4与A1、A2、A3在同一排时，又分两种情况，根据计数原理得到结果．
解答：解：由题意知本题是一个分类和分步原理的综合应用，
A1、A2、A3横向相邻种，在这三种蔬菜的排列就是1×2×3=6种方案；
同时排在上排与排在下排又是两种方案，所以对于A1、A2、A3来说，总共有2×1×2×3=12种方案；对于A6来说，没有任何条件限制，所以在其他五种蔬菜确定后总会有5种可选择的方案；比较复杂的是A4与A5的可以选择的方案．分两种情况：当A4与A1、A2、A3在同一排时，又分两种情况
（1）A1、A2、A3在两边时（左边和右边），A4有两种选择，
由于A4与A5不能相邻，则A5都有4种选择，则方案有2×2×4=16种方案；（2）A1、A2、A3在中间时，A4有两种选择，A4确定后，A5还有5种选择方案，所以，有2×5=10种；当A4与A1、A2、A3不在同一排时，同样分两种情况：（1）A1、A2、A3在两边时（左边和右边），A4有5种选择，但对于A5的选择会有不同
又分三种情况：一是，A4与A1、A2、A3在同一边最边上，A5就有5种选择，1×5=5种；
二是，A4不在最边上，也不在A1、A2、A3的上下相邻的位置时，A5只有3种选择，1×3=3种；
三是，A4在其他3个位置时，A5有4种选择，3×4=12种；
在左边和在右边都一样，所以上面的选择都要乘以2．（2）A1、A2、A3在中间时，A4也有5种选择，A4确定后，A5的选择有4种，共有：5×4=20种；这样，全部可供选择的方案是：12×5×（16+10+20×2+20）=5160．
故选C．
A1、A2、A3横向相邻种，在这三种蔬菜的排列就是1×2×3=6种方案；
同时排在上排与排在下排又是两种方案，所以对于A1、A2、A3来说，总共有2×1×2×3=12种方案；对于A6来说，没有任何条件限制，所以在其他五种蔬菜确定后总会有5种可选择的方案；比较复杂的是A4与A5的可以选择的方案．分两种情况：当A4与A1、A2、A3在同一排时，又分两种情况
（1）A1、A2、A3在两边时（左边和右边），A4有两种选择，
由于A4与A5不能相邻，则A5都有4种选择，则方案有2×2×4=16种方案；（2）A1、A2、A3在中间时，A4有两种选择，A4确定后，A5还有5种选择方案，所以，有2×5=10种；当A4与A1、A2、A3不在同一排时，同样分两种情况：（1）A1、A2、A3在两边时（左边和右边），A4有5种选择，但对于A5的选择会有不同
又分三种情况：一是，A4与A1、A2、A3在同一边最边上，A5就有5种选择，1×5=5种；
二是，A4不在最边上，也不在A1、A2、A3的上下相邻的位置时，A5只有3种选择，1×3=3种；
三是，A4在其他3个位置时，A5有4种选择，3×4=12种；
在左边和在右边都一样，所以上面的选择都要乘以2．（2）A1、A2、A3在中间时，A4也有5种选择，A4确定后，A5的选择有4种，共有：5×4=20种；这样，全部可供选择的方案是：12×5×（16+10+20×2+20）=5160．
故选C．
点评：本题考查计数原理的综合应用，本题解题的关键是对于题目中的分类和分步要做到不重不漏，本题是一个比较困难的排列组合问题，是一个易错题．
练习册系列答案
相关题目
