题目内容
4.曲线y=x3-3x过点(1,-2)的切线条数为( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 设切点坐标为P(t,-3t+t3),再结合导数的几何意义即可求出切线的斜率,再根据过点(1,-2)和切点的斜率等于切线的斜率,列出方程,求出斜率k,根据斜率的个数即可判断切线的条数,从而得到答案.
解答 解:设切点P(t,t3-3t),
由y=x3-3x,则y′=3x2-3,
即有在点P处切线的斜率为k=y′|x=t=3t2-3,
则有在点P处切线方程为y-t3+3t=(3t2-3)(x-t),
又切线过点(1,-2),
即有-2-t3+3t=(3t2-3)(1-t),
即为2t3-3t2+1=0,
即有(t-1)2(2t+1)=0,
解得t=1或-$\frac{1}{2}$,
即t有两个解,即k有两个解,
则过点(1,-2)与曲线相切的切线的条数是2.
故选B.
点评 本题考查了利用导数研究曲线上某点处切线的方程.解题时要特别注意是“在”还是“过”,若是不能确定是否是切点,则设出切点进行求解.此类问题是易错题,关键要注意审题.属于基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
16.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则$\frac{a}{b}$的值( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
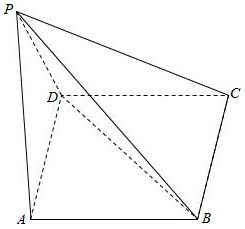 如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.
如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD. 如图,△ABC所在的平面垂直于平面α,D为AB中点,|AB|=2,∠CDB=60°,P为α内的动点,且P到直线CD的距离为$\sqrt{3}$,则AP+BP的值构成的集合为{4}.
如图,△ABC所在的平面垂直于平面α,D为AB中点,|AB|=2,∠CDB=60°,P为α内的动点,且P到直线CD的距离为$\sqrt{3}$,则AP+BP的值构成的集合为{4}.