题目内容
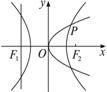
抛物线顶点在原点，准线过双曲线
－
＝1(a＞0，b＞0)的一个焦点，且与双曲线的实轴垂直，已知抛物线与双曲线交点为M
，求抛物线与双曲线方程．
解答：根据已知条件可设抛物线方程为y2＝2px(p＞0)，
∵M
是抛物线与双曲线的交点，则3p＝6，即p＝2，所求抛物线方程为y2＝4x.
由所求抛物线方程可知双曲线的两个焦点分别为F1(－1,0)，F2(1,0)，即c＝1，
又|MF1|＝ 
＝
，|MF2|＝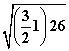 
＝
，
因此|MF1|－|MF2|＝2a，即a＝
，b2＝c2－a2＝
，所求双曲线方程为4x2－
＝1
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
=1的一个焦点，且与双曲线实轴垂直，已知抛物线与双曲线的交点为(
,
)，求抛物线与双曲线的方程.
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为(
,
),求抛物线与双曲线的方程.