题目内容
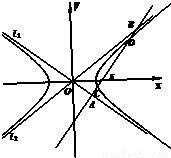
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率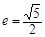 .
.
(1)求证: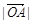 ,
,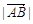 ,
,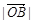 依次成等差数列;
依次成等差数列;
(2)若F(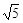 ,0),求直线AB在双曲线上所截得的弦CD的长度.
,0),求直线AB在双曲线上所截得的弦CD的长度.
【答案】
解:(1)由已知e2=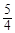 ,即
,即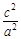 =
=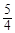 ,故a2=
,故a2=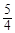 c2,
①
c2,
①
从而b2=c2-a2=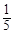 c2, ②
c2, ②
故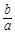 =
=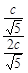 =
=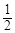 ,设∠AOF=∠BOF=
,设∠AOF=∠BOF=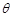 ,
,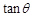 =
=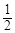 .
.
故tan∠AOB=tan2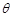 =
= =
=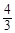 ,即
,即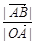 =
=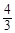 .
.
令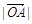 =3m(m>0) ,则
=3m(m>0) ,则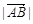 =4m,
=4m,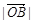 =5m,满足
=5m,满足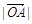 +
+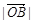 =2
=2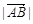 ,
,
所以,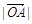 ,
,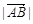 ,
,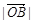 依次成等差数列.
依次成等差数列.
(2)由已知c2=5,代入①,②得a2=4, b2=1,
于是双曲线的方程为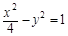 .
.
设直线AB的斜率为k,则k=tan∠BFx=tan∠AFO=cot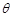 =2.
=2.
于是直线AB的议程为 y=2(x-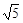 ).…………………………………………9分
).…………………………………………9分
联立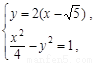 消y得15x2-
消y得15x2-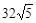 x+84=0.
x+84=0.
故弦CD的长度 | CD |=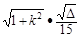 =
=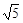 ×
×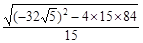 =
=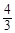 …13分
…13分
【解析】略

练习册系列答案
相关题目
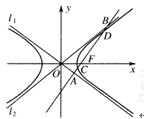
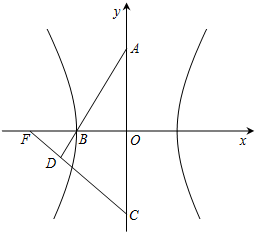 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )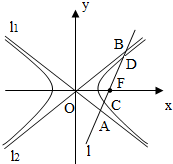 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率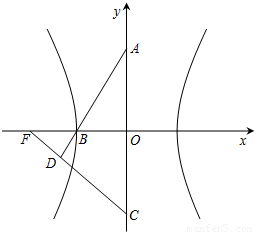
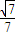
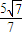
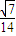
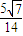
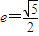 .
.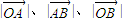 依次成等差数列;
依次成等差数列;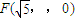 ,求直线AB在双曲线上所截得的弦CD的长度.
,求直线AB在双曲线上所截得的弦CD的长度.