题目内容
已知函数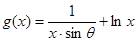 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且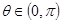 ,
,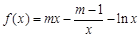 ,
, ∈R.
∈R.
(1)求θ的值;
(2)若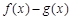 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得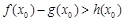 成立,求
成立,求 的取值范围.
的取值范围.
【答案】
(1)由题意,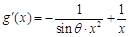 ≥0在
≥0在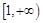 上恒成立,即
上恒成立,即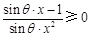 .
.
∵θ∈(0,π),∴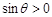 .故
.故 在
在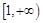 上恒成立,
上恒成立,
只须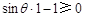 ,即
,即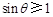 ,只有
,只有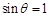 .结合θ∈(0,π),得
.结合θ∈(0,π),得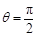 .…4分
.…4分
(2)由(1),得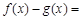
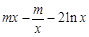 .
.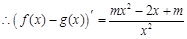 .
.
∵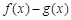 在其定义域内为单调函数,
在其定义域内为单调函数,
∴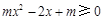 或者
或者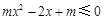 在[1,+∞)恒成立.…………6分
在[1,+∞)恒成立.…………6分
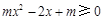 等价于
等价于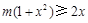 ,即
,即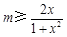 ,
,
而 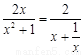 ,(
,(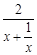 )max=1,∴
)max=1,∴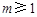 . ………………………7分
. ………………………7分
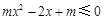 等价于
等价于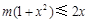 ,即
,即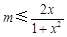 在[1,+∞)恒成立,
在[1,+∞)恒成立,
而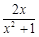 ∈(0,1],
∈(0,1],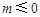 .
.
综上,m的取值范围是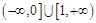 .……………………………9分
.……………………………9分
(3)构造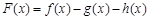 ,
,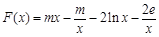 .
.
当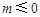 时,
时,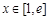 ,
,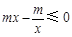 ,
,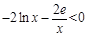 ,所以在[1,e]上不存在一个
,所以在[1,e]上不存在一个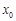 使得
使得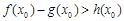 成立. ………………………………11分
成立. ………………………………11分
当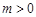 时,
时,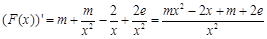 .
.
因为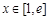 ,所以
,所以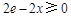 ,
,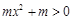 ,所以
,所以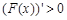 在
在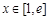 恒成立.
恒成立.
故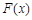 在
在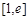 上单调递增,
上单调递增,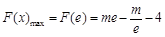 ,只要
,只要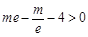 ,
,
解得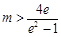
故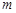 的取值范围是
的取值范围是 .
.
【解析】略

练习册系列答案
相关题目
 在[-1,+ ∞)上是减函数,则a的取值范围是
.
在[-1,+ ∞)上是减函数,则a的取值范围是
. 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R. 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围; ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, 的值;
的值; 在[1,+∞)上为单调函数,求实数
在[1,+∞)上为单调函数,求实数 的取值范围;
的取值范围; 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.
 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.