题目内容
设椭圆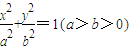 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆和x轴正半轴于P,Q两点,且AP:PQ=8:5.
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆和x轴正半轴于P,Q两点,且AP:PQ=8:5.(1)求椭圆的离心率;
(2)已知直线l过点M(-3,0),倾斜角为
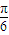 ,圆C过A,Q,F三点,若直线l恰好与圆C相切,求椭圆方程.
,圆C过A,Q,F三点,若直线l恰好与圆C相切,求椭圆方程.
【答案】分析:(1)设出P,Q,F坐标,利用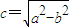 以及AP:PQ=8:5,求出P的坐标代入椭圆方程,即可求椭圆的离心率;
以及AP:PQ=8:5,求出P的坐标代入椭圆方程,即可求椭圆的离心率;
(2)利用直线l过点M(-3,0),倾斜角为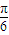 ,求出直线的方程,通过圆C过A,Q,F三点,直线l恰好与圆C相切,圆心到直线的距离等于半径,求出a,b,c的值,即可求得椭圆方程.
,求出直线的方程,通过圆C过A,Q,F三点,直线l恰好与圆C相切,圆心到直线的距离等于半径,求出a,b,c的值,即可求得椭圆方程.
解答:解:(1)设点Q(x,0),F(-c,0),P(x,y),其中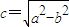 ,A(0,b).
,A(0,b).
由AP:PQ=8:5,得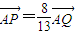 ,
,
即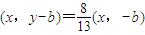 ,得
,得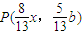 ,…(2分)
,…(2分)
点P在椭圆上,∴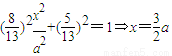 .①…(4分)
.①…(4分)
而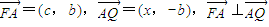 ,
,
∴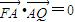 .
.
∴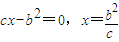 .②…(6分)
.②…(6分)
由①②知2b2=3ac,
∴2c2+3ac-2a2=0.
∴2e2+3e-2=0,
∴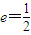 . …(8分)
. …(8分)
(2)由题意,得直线l的方程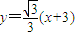 ,即
,即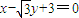 ,
,
满足条件的圆心为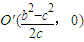 ,
,
又a=2c,∴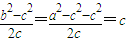 ,∴O′(c,0). …(10分)
,∴O′(c,0). …(10分)
圆半径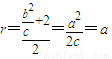 . …(12分)
. …(12分)
由圆与直线l: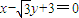 相切得,
相切得,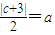 ,…(14分)
,…(14分)
又a=2c,∴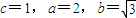 .
.
∴椭圆方程为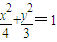 . …(16分)
. …(16分)
点评:本题是中档题,考查题意的离心率的求法,直线与圆的位置关系的应用,椭圆方程的求法,考查计算能力,转化思想,常考题型.
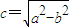 以及AP:PQ=8:5,求出P的坐标代入椭圆方程,即可求椭圆的离心率;
以及AP:PQ=8:5,求出P的坐标代入椭圆方程,即可求椭圆的离心率;(2)利用直线l过点M(-3,0),倾斜角为
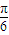 ,求出直线的方程,通过圆C过A,Q,F三点,直线l恰好与圆C相切,圆心到直线的距离等于半径,求出a,b,c的值,即可求得椭圆方程.
,求出直线的方程,通过圆C过A,Q,F三点,直线l恰好与圆C相切,圆心到直线的距离等于半径,求出a,b,c的值,即可求得椭圆方程.解答:解:(1)设点Q(x,0),F(-c,0),P(x,y),其中
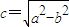 ,A(0,b).
,A(0,b).由AP:PQ=8:5,得
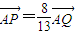 ,
,即
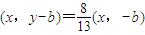 ,得
,得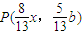 ,…(2分)
,…(2分)点P在椭圆上,∴
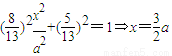 .①…(4分)
.①…(4分)而
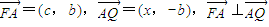 ,
,∴
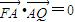 .
.∴
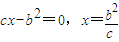 .②…(6分)
.②…(6分)由①②知2b2=3ac,
∴2c2+3ac-2a2=0.
∴2e2+3e-2=0,
∴
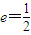 . …(8分)
. …(8分)(2)由题意,得直线l的方程
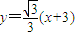 ,即
,即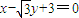 ,
,满足条件的圆心为
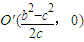 ,
,又a=2c,∴
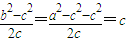 ,∴O′(c,0). …(10分)
,∴O′(c,0). …(10分)圆半径
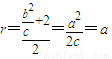 . …(12分)
. …(12分)由圆与直线l:
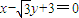 相切得,
相切得,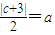 ,…(14分)
,…(14分)又a=2c,∴
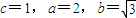 .
.∴椭圆方程为
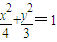 . …(16分)
. …(16分)点评:本题是中档题,考查题意的离心率的求法,直线与圆的位置关系的应用,椭圆方程的求法,考查计算能力,转化思想,常考题型.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
(本小题满分12分)
设椭圆![]() 的左焦点为F,O为坐标原点,已知椭圆中心关于直线
的左焦点为F,O为坐标原点,已知椭圆中心关于直线![]() 对称点恰好落在椭圆的左准线上。
对称点恰好落在椭圆的左准线上。
(1)求过O、F并且与椭圆右准线l相切的圆的方程;
|

 外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。
外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。 ,求直线
,求直线 的方程。
的方程。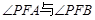 是否总是相等?若是,请给出证明。
是否总是相等?若是,请给出证明。 的左焦点为F, 离心率为
的左焦点为F, 离心率为 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. 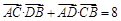 , 求k的值.
, 求k的值.