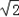题目内容
设椭圆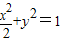 上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为( )
上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为( )A.

B.

C.
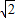
D.2
【答案】分析:设直线OP方程为y=kx,点P(x1,y1),利用方程组联解的方法可得: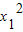 =
=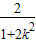 ,
,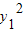 =
=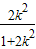 ,所以r12=
,所以r12=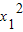 +
+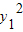 =
=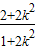 .同理可得到Q(x2,y2)满足:r22=
.同理可得到Q(x2,y2)满足:r22=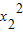 +
+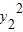 =
=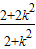 ,所以有
,所以有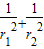 =
= ,化简整理,结合基本不等式,可得r1r2≥
,化简整理,结合基本不等式,可得r1r2≥ ,当且仅当r1=r2,即k2=1时,r1r2取到最小值
,当且仅当r1=r2,即k2=1时,r1r2取到最小值 .
.
解答:解:设直线OP方程为y=kx,点P(x1,y1)
∵点P是椭圆 与直线y=kx的交点
与直线y=kx的交点
∴由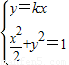 可得:
可得: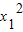 =
=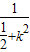 =
=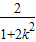 ,
,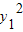 =k2x2=
=k2x2=
∵点P与原点O的距离为|OP|=r1,
∴r12=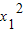 +
+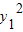 =
=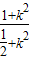 =
=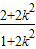 ,
,
∵OQ是由OP绕原点逆时针旋转90°而得,
∴直线OQ方程为y=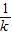 x,
x,
再设Q(x2,y2),用类似于求r12的方法,可得r22=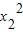 +
+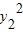 =
=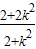
∴r1、r2满足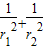 =
= ,可得
,可得 +
+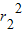 =
=
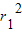
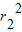
根据基本不等式,可得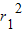 +
+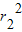 ≥2r1r2
≥2r1r2
∴
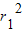
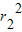 ≥2r1r2,即r1r2≥
≥2r1r2,即r1r2≥ ,当且仅当r1=r2,即k2=1时,r1r2取到最小值
,当且仅当r1=r2,即k2=1时,r1r2取到最小值
故选B
点评:本题给出椭圆上两点P、Q满足∠POQ=90°,求OP、OQ之积的最小值,着重考查了椭圆的基本概念、直线与椭圆的关系和基本不等式等知识点,属于中档题.
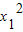 =
=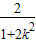 ,
,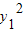 =
=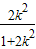 ,所以r12=
,所以r12=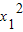 +
+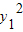 =
=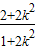 .同理可得到Q(x2,y2)满足:r22=
.同理可得到Q(x2,y2)满足:r22=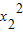 +
+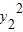 =
=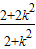 ,所以有
,所以有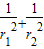 =
= ,化简整理,结合基本不等式,可得r1r2≥
,化简整理,结合基本不等式,可得r1r2≥ ,当且仅当r1=r2,即k2=1时,r1r2取到最小值
,当且仅当r1=r2,即k2=1时,r1r2取到最小值 .
.解答:解:设直线OP方程为y=kx,点P(x1,y1)
∵点P是椭圆
 与直线y=kx的交点
与直线y=kx的交点∴由
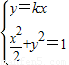 可得:
可得: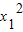 =
=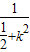 =
=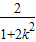 ,
,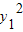 =k2x2=
=k2x2=
∵点P与原点O的距离为|OP|=r1,
∴r12=
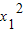 +
+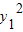 =
=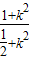 =
=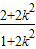 ,
,∵OQ是由OP绕原点逆时针旋转90°而得,
∴直线OQ方程为y=
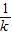 x,
x,再设Q(x2,y2),用类似于求r12的方法,可得r22=
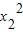 +
+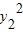 =
=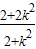
∴r1、r2满足
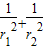 =
= ,可得
,可得 +
+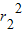 =
=
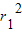
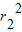
根据基本不等式,可得
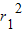 +
+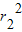 ≥2r1r2
≥2r1r2∴

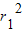
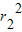 ≥2r1r2,即r1r2≥
≥2r1r2,即r1r2≥ ,当且仅当r1=r2,即k2=1时,r1r2取到最小值
,当且仅当r1=r2,即k2=1时,r1r2取到最小值
故选B
点评:本题给出椭圆上两点P、Q满足∠POQ=90°,求OP、OQ之积的最小值,着重考查了椭圆的基本概念、直线与椭圆的关系和基本不等式等知识点,属于中档题.

练习册系列答案
相关题目
 上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为
上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为


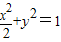 上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为( )
上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为( )

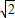
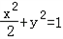 上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为
上一点P与原点O的距离为|OP|=r1,OP的倾斜角为θ,将射线OP绕原点O逆时针旋转90°后与椭圆相交于点Q,若|OQ|=r2,则r1r2的最小值为