题目内容
用32m2 的材料制作一个长方体形的无盖盒子,如果底面的宽规定为2m,那么这个盒子的最大容积可以是( )
| A、36m3 | B、18m3 | C、16m3 | D、14m3 |
分析:设出长方体底面边长xm,高hm,由底面宽为2m,可表示出体积v;由长方体无盖,可得x,h的关系,消去h,得v,x的函数,求出v的最值.
解答: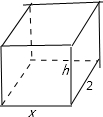 解:如图,设长方体底面的边长为xm,高为hm,体积为vm3,那么,
解:如图,设长方体底面的边长为xm,高为hm,体积为vm3,那么,
表面积为:2x+2hx+4h=32,∴h=
,(且0<x<16);
体积为:v=2x•h=
=
,令t=x+2>2,
则v=
=40-2(t+
)≤40-2×2
=16,当且仅当t=6时,“=”成立;
故应选:C.
 解:如图,设长方体底面的边长为xm,高为hm,体积为vm3,那么,
解:如图,设长方体底面的边长为xm,高为hm,体积为vm3,那么,表面积为:2x+2hx+4h=32,∴h=
| 16-x |
| x+2 |
体积为:v=2x•h=
| 2x(16-x) |
| x+2 |
| 32x-2x2 |
| x+2 |
则v=
| 32(t-2)-2(t-2)2 |
| t |
| 36 |
| t |
t•
|
故应选:C.
点评:本题用长方体的表面积和体积,建立函数解析式,求出函数的最值,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
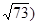 m2 B.16 m2
m2 B.16 m2
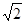 m2
D.14 m2
m2
D.14 m2