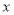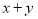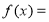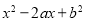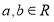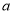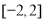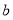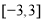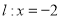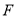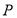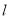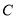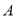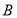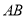题目内容
设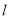 是一条直线,
是一条直线,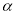 ,
,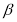 ,
,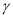 是不同的平面,则下列说法不正确的是( )
是不同的平面,则下列说法不正确的是( )
A.如果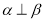 ,那么
,那么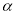 内一定存在直线平行于
内一定存在直线平行于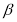
B.如果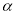 不垂直于
不垂直于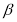 ,那么
,那么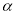 内一定不存在直线垂直于
内一定不存在直线垂直于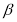
C.如果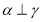 ,
,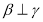 ,
,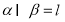 ,那么
,那么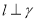
D.如果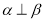 ,
,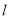 与
与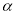 ,
,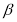 都相交,那么
都相交,那么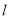 与
与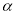 ,
,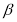 所成的角互余
所成的角互余
D
【解析】
试题分析:对于A,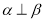 ,说明这两个平面必相交,设其交线为
,说明这两个平面必相交,设其交线为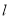 ,任意直线
,任意直线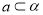 且
且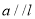 ,由平面的基本性质可知
,由平面的基本性质可知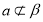 ,所以由线面平行的判定定理可判定
,所以由线面平行的判定定理可判定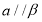 ,正确;对于B,假设
,正确;对于B,假设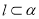 且
且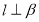 ,则由面面垂直的判定定理可得
,则由面面垂直的判定定理可得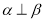 ,这与条件
,这与条件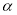 不垂直于
不垂直于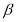 相矛盾,假设不正确,故B也正确;对于C,如下图(1),设
相矛盾,假设不正确,故B也正确;对于C,如下图(1),设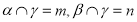 ,在平面
,在平面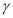 内取一点
内取一点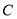 ,作
,作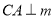 于点
于点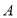 ,
,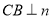 于点
于点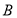 ,则由面面垂直:
,则由面面垂直: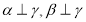 的性质可得
的性质可得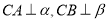 ,而
,而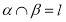 ,所以
,所以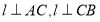 ,由线面垂直的判定定理可得
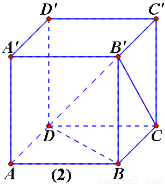
,由线面垂直的判定定理可得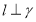 ,故C选项正确;对于D,这是不成立的,如下图(2)的长方体,设
,故C选项正确;对于D,这是不成立的,如下图(2)的长方体,设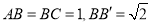 ,分别记平面
,分别记平面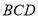 、平面
、平面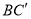 为
为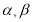 ,记直线
,记直线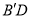 为
为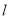 ,则
,则 与平面
与平面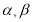 所成的角分别为
所成的角分别为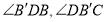 ,而
,而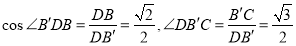 ,故
,故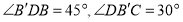 ,
,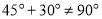 ,故D选项不正确,选D.
,故D选项不正确,选D.

考点:1.空间中的平行、垂直问题;2.线面角.

练习册系列答案
相关题目