题目内容
设Sn为数列{an}的前n项和，若
（n∈N+）是非零常数，则称该数列为“和等比数列”，若数列{Cn}是首项为2，公差为d（d≠0）的等差数列，且数列{Cn}是“和等比数列”，则d=________．
4
分析：由题意设数列{Cn}的前n项和为Tn，可得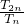
=
=k，对于n∈N*都成立，化简得，（k-4）dn+（k-2）（4-d）=0，由题意可得4-d=0，解之即可．
解答：由题意设数列{Cn}的前n项和为Tn，
则Tn=2n+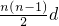
，T2n=4n+
，
因为数列{Cn}是“和等比数列”，
所以=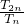
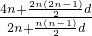==k，对于n∈N*都成立，
化简得，（k-4）dn+（k-2）（4-d）=0，
因为d≠0，故只需4-d=0，解得d=4
故答案为：4
点评：本题考查等差数列与等比数列的综合应用，涉及新定义，属基础题．
分析：由题意设数列{Cn}的前n项和为Tn，可得
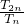==k，对于n∈N*都成立，化简得，（k-4）dn+（k-2）（4-d）=0，由题意可得4-d=0，解之即可．解答：由题意设数列{Cn}的前n项和为Tn，
则Tn=2n+
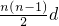，T2n=4n+，因为数列{Cn}是“和等比数列”，
所以
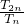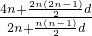===k，对于n∈N*都成立，化简得，（k-4）dn+（k-2）（4-d）=0，
因为d≠0，故只需4-d=0，解得d=4
故答案为：4
点评：本题考查等差数列与等比数列的综合应用，涉及新定义，属基础题．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目