题目内容
如图1,在Rt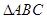 中,
中, 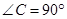 ,
,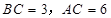 .D、E分别是
.D、E分别是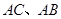 上的点,且
上的点,且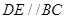 .将
.将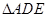 沿
沿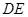 折起到
折起到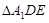 的位置,使
的位置,使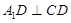 ,如图2.
,如图2.

(Ⅰ)求证: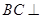 平面
平面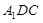 ;
;
(Ⅱ)若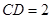 ,求
,求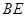 与平面
与平面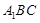 所成角的正弦值;
所成角的正弦值;
【答案】
(1)根据题意,对于线面垂直的证明一般先证明线线垂直,即由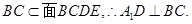
 .
.
(2)
【解析】
试题分析:(Ⅰ)在图1△ 中,
中, .
.
 .
2分
.
2分
又 .4分
.4分
由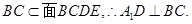
 .
6分
.
6分
(Ⅱ)如图,以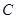 为原点,建立空间直角坐标系. 7分
为原点,建立空间直角坐标系. 7分
 .8分
.8分

设 为平面
为平面 的一个法向量,
的一个法向量,
因为

所以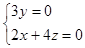 ,
,
令 ,得
,得 .
.
所以 为平面
为平面 的一个法向量.
10分
的一个法向量.
10分
设 与平面
与平面 所成角为
所成角为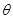 .
.
则 .
.
所以 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .13分
.13分
考点:证明垂直,线面角的求解
点评:主要是考查了运用向量法来求解角和证明垂直,属于基础题。

练习册系列答案
相关题目
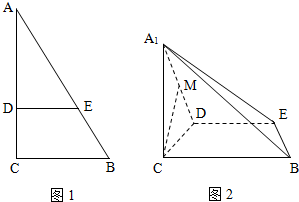 (2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.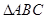 中,
中,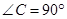 ,
,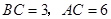 ,D、E分别是
,D、E分别是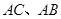 上的点,且
上的点,且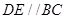 ,将
,将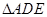 沿
沿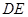 折起到
折起到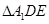 的位置,使
的位置,使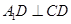 ,如图2.
,如图2.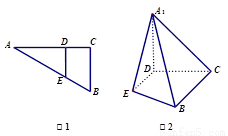
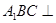 平面
平面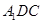 ;
;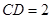 ,求
,求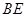 与平面
与平面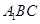 所成角的余弦值;
所成角的余弦值;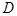 点在何处时,
点在何处时,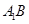 的长度最小,并求出最小值.
的长度最小,并求出最小值. 中,
中,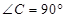 ,
,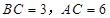 .D、E分别是
.D、E分别是 上的点,且
上的点,且 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.
 平面
平面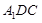 ;
; ,求
,求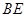 与平面
与平面 所成角的余弦值;
所成角的余弦值;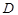 点在何处时,
点在何处时, 的长度最小,并求出最小值.
的长度最小,并求出最小值.