题目内容
 一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).
一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).(1)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,求月收入在[1500,2000)(元)段应抽出的人数;
(2)估计该社区居民月收人的平均数;
(3)为了估计该社区3个居民中恰有2个月收入在[2000,3000)(元)的概率,采用随机模拟的方法:先由计算器算出0到9之间取整数值的随机数,我们用0,1,2,3,…表示收入在[2000,3000)(元)的居民,剩余的数字表示月收入不在[2000,3000)(元)的居民;再以每三个随机数为一组,代表统计的结果,经随机模拟产生了20组随机数如下:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计,计算该社区3个居民中恰好有2个月收入在[2000,3000)(元)的概率.
【答案】分析:(1)观察频率分布直方图,然后根据频率为相应小矩形的面积,即可求出所求;
(2)分别求出每一组的频率,然后根据平均数等于各组的频率乘以组中值的和进行求解即可;
(3)观察上述随机数可得,该社区3个居民中恰有2个月收入在[2000,3000)元的个数,然后根据古典概型的概率公式解之.
解答:解:(1)由频率分布直方图可知,月收入在[1500,2000)的频率为0.0004×500=0.2
所以应抽取的人数为0.2×100=20人
(2)由频率分布直方图可知,月收入在[1000,1500)的频率为0.1
月收入在[1500,2000)的频率为0.2
月收入在[2000,2500)的频率为0.25
月收入在[2500,3000)的频率为0.25
月收入在[3000,3500)的频率为0.15
月收入在[3500,4000)的频率为0.05
所以估计月收入的平均数为:0.1×1250+0.2×1750+0.25×2250+0.25×2750+0.15×3250+0.05×3750=2400元
(3)由频率分布直方图可知,月收入在[2000,3000)的频率为2×0.0005×500=0.5
可以用数字0,1,2,3,4表示收入在[2000,3000)(元)的居民,数字5,6,7,8,9表示月收入不在[2000,3000)(元)的居民;
观察上述随机数可得,该社区3个居民中恰有2个月在[2000,3000)的有191,271,932,812,393,027,730,共有7个
而基本事件一共有20个,根据古典概型公式可知该社区3个居民中恰有2个月收入在[2000,3000)元的概率为P= =0.35
=0.35
点评:本题主要考查了频率分布直方图,以及古典概型的概率,同时考查了读图能力和运算求解能力,属于基础题.
(2)分别求出每一组的频率,然后根据平均数等于各组的频率乘以组中值的和进行求解即可;
(3)观察上述随机数可得,该社区3个居民中恰有2个月收入在[2000,3000)元的个数,然后根据古典概型的概率公式解之.
解答:解:(1)由频率分布直方图可知,月收入在[1500,2000)的频率为0.0004×500=0.2
所以应抽取的人数为0.2×100=20人
(2)由频率分布直方图可知,月收入在[1000,1500)的频率为0.1
月收入在[1500,2000)的频率为0.2
月收入在[2000,2500)的频率为0.25
月收入在[2500,3000)的频率为0.25
月收入在[3000,3500)的频率为0.15
月收入在[3500,4000)的频率为0.05
所以估计月收入的平均数为:0.1×1250+0.2×1750+0.25×2250+0.25×2750+0.15×3250+0.05×3750=2400元
(3)由频率分布直方图可知,月收入在[2000,3000)的频率为2×0.0005×500=0.5
可以用数字0,1,2,3,4表示收入在[2000,3000)(元)的居民,数字5,6,7,8,9表示月收入不在[2000,3000)(元)的居民;
观察上述随机数可得,该社区3个居民中恰有2个月在[2000,3000)的有191,271,932,812,393,027,730,共有7个
而基本事件一共有20个,根据古典概型公式可知该社区3个居民中恰有2个月收入在[2000,3000)元的概率为P=
 =0.35
=0.35点评:本题主要考查了频率分布直方图,以及古典概型的概率,同时考查了读图能力和运算求解能力,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
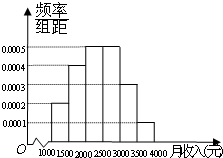 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图). (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).
