题目内容
给出如下四个命题
①对于任意的实数α和β,等式cos(α+β)=cosαcosβ-sinαsinβ恒成立;
②存在实数α,β,使等式cos(α+β)=cosαcosβ+sinαsinβ能成立;
③公式tan(α+β)=
成立的条件是α≠kπ+
(k∈Z)且β≠kπ+
(k∈Z);
④不存在无穷多个α和β,使sin(α-β)=sinαcosβ-cosαsinβ;
其中假命题是( )
①对于任意的实数α和β,等式cos(α+β)=cosαcosβ-sinαsinβ恒成立;
②存在实数α,β,使等式cos(α+β)=cosαcosβ+sinαsinβ能成立;
③公式tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
| π |
| 2 |
| π |
| 2 |
④不存在无穷多个α和β,使sin(α-β)=sinαcosβ-cosαsinβ;
其中假命题是( )
| A、①② | B、②③ | C、③④ | D、②③④ |
分析:①此等式是两角和的余弦函数公式,本选项为真命题;
②存在α与β的值,使等式成立,本选项为真命题;
③公式成立还得对α+β进行限制,本选项为假命题;
④此等式为两角差的正弦函数公式,所以对无穷多个α和β成立,本选项为假命题.
②存在α与β的值,使等式成立,本选项为真命题;
③公式成立还得对α+β进行限制,本选项为假命题;
④此等式为两角差的正弦函数公式,所以对无穷多个α和β成立,本选项为假命题.
解答:解:①此公式为两角和的余弦函数公式,本选项为真命题;
②α=
,β=0时,cos(
+0)=0,而cos
cos0+sin
sin0=0,等式成立,本选项为真命题;
③此公式成立需满足α≠kπ+
(k∈Z)且β≠kπ+
(k∈Z)且α+β≠kπ+
,本选项为假命题;;
④此公式为两角差的正弦函数公式,对任意的α和β都满足,本选项为假命题.
综上,假命题的序号有:③④.
故答案为:③④
②α=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
③此公式成立需满足α≠kπ+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
④此公式为两角差的正弦函数公式,对任意的α和β都满足,本选项为假命题.
综上,假命题的序号有:③④.
故答案为:③④
点评:此题考查学生掌握两角和与差的正弦、余弦函数公式,掌握正切函数成立时满足的条件,是一道基础题.

练习册系列答案
相关题目
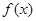 ,如果存在函数
,如果存在函数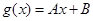 (A、B为常数),使得
(A、B为常数),使得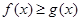 对一切实数
对一切实数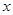 都成立,那么称
都成立,那么称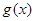 为函数
为函数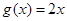 为函数
为函数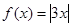 的一个承托函数;④
的一个承托函数;④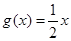 为函数
为函数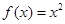 的一个承托函数。其中正确的命题有
。
的一个承托函数。其中正确的命题有
。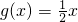 为函数f(x)=x2的一个承托函数.其中正确的命题有________.
为函数f(x)=x2的一个承托函数.其中正确的命题有________. 为函数f(x)=x2的一个承托函数.其中正确的命题有 .
为函数f(x)=x2的一个承托函数.其中正确的命题有 .