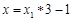题目内容
定义某种运算 ,
, 的运算原理如图所示.设
的运算原理如图所示.设 .则
.则 ______;
______; 在区间
在区间 上的最小值为______.
上的最小值为______.
 ,
, 的运算原理如图所示.设
的运算原理如图所示.设 .则
.则 ______;
______; 在区间
在区间 上的最小值为______.
上的最小值为______.
 ;
;
通过程序框图判断出S=a?b的解析式,再求出f(x)的解析式,从而求出f(2)的值;最后根据所求出f(x)的解析式结合图象求解f(x)在区间[-2,2]上的最小值即可.
解答:解:∵由流程图可知,运算S=a?b中S的值等于分段函数 S= 的函数值,
的函数值,
∴f(2)=(0?2)2-(2?2)
=0×2-2=-2.
且f(x)=(0?x)x-(2?x)= ,
,
画出它的图象,如图所示,
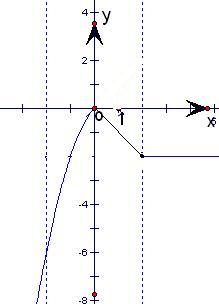
由图可知,当x=-2时,f(x)在区间[-2,2]上的最小值为-6.
故答案为:-2;-6.
解答:解:∵由流程图可知,运算S=a?b中S的值等于分段函数 S=
 的函数值,
的函数值,∴f(2)=(0?2)2-(2?2)
=0×2-2=-2.
且f(x)=(0?x)x-(2?x)=
 ,
,画出它的图象,如图所示,

由图可知,当x=-2时,f(x)在区间[-2,2]上的最小值为-6.
故答案为:-2;-6.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 ”表示的功能描述正确的一项是( )
”表示的功能描述正确的一项是( ) ,
, 
 ,
, 






 ,
,
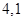 B.
B.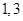 C.
C.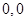 D.
D. 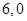
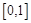 产生的均匀随机数
产生的均匀随机数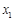 ,转化为
,转化为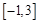 上的均匀随机数
上的均匀随机数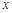 ,实施的变换为
,实施的变换为