题目内容
有人预测:在2010年的广州亚运会上,排球比赛的决赛将在中国队与日本队之间展开,据以往统计,中国队在每局比赛中胜日本队的概率为 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(1)求中国队以3:1获胜的概率.
(2)设ξ表示比赛的局数,求ξ的分布列与数学期望.
【答案】分析:(1)由题意知本题的比赛,每一局之间都是不影响的,且中国队获胜的概率都相同,符合独立重复试验,根据独立重复试验的概率公式写出中国队乙三比一获胜的概率.即前三场中国队胜两场,且第四场一定胜.
(2)ξ表示比赛的局数,则ξ的所有可能取值为3,4,5.结合变量对应的事件和第一问的分析写出变量的概率,当变量等于5时,可以用1减去前两个变量的概率得到结果,写出分布列,做出数学期望.
解答:解:(1)由题意知本题的比赛,每一局之间都是不影响的,
且中国队获胜的概率都相同,符合独立重复试验,
设“中国队以3:1获胜”为事件A,
则事件A表示“前3局中国队恰好胜2局,然后第4局胜”,
∴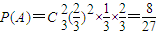 .
.
(2)ξ的所有可能取值为3,4,5.
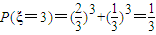 ;
;
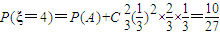 ;
;
P(ξ=5)=1-P(ξ=3)-P(ξ=4)=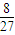 .
.
∴ξ的分布列为:
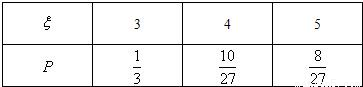
∴ξ的数学期望为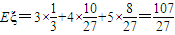 .
.
点评:本题考查独立重复试验,考查离散型随机变量的分布列和期望,考查利用概率知识解决实际问题的能力,是一个综合题目,这种题目可以作为理科的一道解答题目出现.
(2)ξ表示比赛的局数,则ξ的所有可能取值为3,4,5.结合变量对应的事件和第一问的分析写出变量的概率,当变量等于5时,可以用1减去前两个变量的概率得到结果,写出分布列,做出数学期望.
解答:解:(1)由题意知本题的比赛,每一局之间都是不影响的,
且中国队获胜的概率都相同,符合独立重复试验,
设“中国队以3:1获胜”为事件A,
则事件A表示“前3局中国队恰好胜2局,然后第4局胜”,
∴
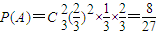 .
.(2)ξ的所有可能取值为3,4,5.
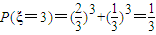 ;
;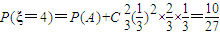 ;
;P(ξ=5)=1-P(ξ=3)-P(ξ=4)=
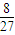 .
.∴ξ的分布列为:

∴ξ的数学期望为
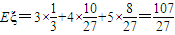 .
.点评:本题考查独立重复试验,考查离散型随机变量的分布列和期望,考查利用概率知识解决实际问题的能力,是一个综合题目,这种题目可以作为理科的一道解答题目出现.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.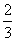 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛。
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛。 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛. ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.