题目内容
(本题满分12分)已知不等式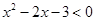 的解集为
的解集为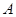 ,不等式
,不等式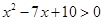 的解集为
的解集为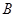 .
.
(Ⅰ) 求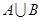 ;
;
(Ⅱ)若不等式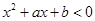 的解集为
的解集为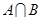 ,求
,求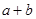 的值.
的值.
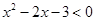 的解集为
的解集为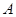 ,不等式
,不等式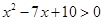 的解集为
的解集为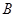 .
.(Ⅰ) 求
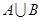 ;
; (Ⅱ)若不等式
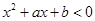 的解集为
的解集为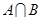 ,求
,求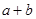 的值.
的值.(I)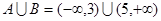 .(Ⅱ)
.(Ⅱ)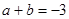 .
.
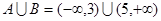 .(Ⅱ)
.(Ⅱ)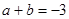 .
.试题分析:(1)由题意利用一元二次方程的解法分别求出集合A和B,然后利用集合的并集定义进行求解;
(2)已知不等式ax2-x+b<0的解集为A
 B,可以求出a,b的值,然后把其代入不等式x2+ax+b>0进行求解;
B,可以求出a,b的值,然后把其代入不等式x2+ax+b>0进行求解;解:由
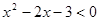 得
得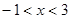 ,所以
,所以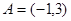 .………… 2分
.………… 2分由
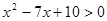 得
得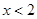 或
或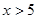 ,所以
,所以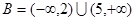 .………… 4分
.………… 4分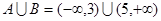 . …………6分
. …………6分(Ⅱ)由(Ⅰ)知
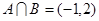 …………7分
…………7分则不等式
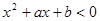 的解集为
的解集为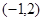 ,即
,即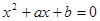 的根为-1,2,…………9分
的根为-1,2,…………9分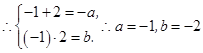 ,…………11分
,…………11分即
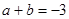 .………… 12分
.………… 12分点评:解决该试题的关键是一元二次不等式的准确求解,并能利用韦达定理得到系数的值,进而求解得到。

练习册系列答案
相关题目
 ,且
,且 ,则集合
,则集合 可能是
可能是


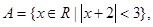 集合
集合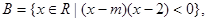 且
且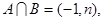 则
则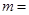 __________,
__________,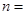 __________.
__________.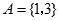 ,
,  ,则
,则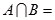 ( )
( )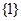
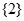
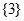
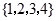
 ,
,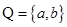 ,若
,若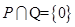 ,则
,则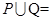 ( )
( )
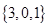
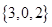

 ,
, ,那么
,那么 等于( )
等于( )



 ,
, ,则
,则 = .
= .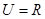 ,且
,且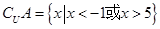 ,
,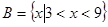 ,求:A∩B;A∪B
,求:A∩B;A∪B