题目内容
(3分)(2011•重庆)若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=4,且C=60°,则ab的值为( )
A. | B. | C.1 | D. |
A
解析试题分析:将已知的等式展开;利用余弦定理表示出a2+b2﹣c2求出ab的值.
解:∵(a+b)2﹣c2=4,
即a2+b2﹣c2+2ab=4,
由余弦定理得2abcosC+2ab=4,
∵C=60°,
∴ ,
,
故选A.
点评:本题考查三角形中余弦定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在 中,角
中,角 的对边分别为
的对边分别为 ,若点
,若点 在直线
在直线 上,则角
上,则角 的值为( )
的值为( )
A. | B. | C. | D. |
在 中,
中, 分别为角
分别为角 的对边,
的对边, ,则
,则 的形状为( )
的形状为( )
| A.正三角形 | B.直角三角形 | C.等腰直角三角形 | D.等腰三角形 |
在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为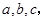 若
若 ,则角B的值为( )
,则角B的值为( )
A. | B. | C. | D. |
 ,那么b=
,那么b= B.
B. C.
C. D.
D.
 两地相距
两地相距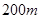 ,且
,且 地在
地在 地的正东方。一人在
地的正东方。一人在 在正北方,建筑
在正北方,建筑 在北偏西
在北偏西 ;在
;在 ,建筑
,建筑 ,则两建筑
,则两建筑



 m B.400 m C.200
m B.400 m C.200 m D.500 m
m D.500 m sinA-cos(B+
sinA-cos(B+ )的最大值为( )
)的最大值为( )
 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )


