题目内容
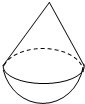
如图是在一个半球上面放一个圆锥，其中圆锥的底面与半球的底面重合，且圆锥的体积与半球体积相等，则圆锥的轴截面两条母线的夹角为arccos
| 3 |
| 5 |
arccos
．（结果用反三角函数表示）| 3 |
| 5 |
分析：先设圆锥的半径为R，高为H，母线与轴所成角为θ，求出圆锥的高，然后利用体积相等建立等式关系，求出2θ的余弦值，最后用反三角表示即可．
解答：解：设圆锥的半径为R，高为H，母线与轴所成角为θ，则圆锥的高 H=R•cotθ
圆锥的体积 V1=
πR2•H=
πR3cotθ
半球的体积 V2=
πR3
∵V1=V2即：
πR3cotθ=
πR3
∴cotθ=2
∴cos2θ=
即圆锥的轴截面两条母线的夹角为arccos
故答案为：arccos
．
圆锥的体积 V1=
| 1 |
| 3 |
| 1 |
| 3 |
半球的体积 V2=
| 2 |
| 3 |
∵V1=V2即：
| 1 |
| 3 |
| 2 |
| 3 |
∴cotθ=2
∴cos2θ=
| 3 |
| 5 |
即圆锥的轴截面两条母线的夹角为arccos
| 3 |
| 5 |
故答案为：arccos
| 3 |
| 5 |
点评：本题考查旋转体圆锥、球的体积，以及三角函数的求值，考查计算能力，属于基础题．
练习册系列答案
相关题目
