题目内容
 在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO
在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO
(1)求证:AO⊥平面FEBC
(2)求证:四边形BCFE为正方形.
解:(1)证明:因为四边形BCFE是菱形,所以BF⊥EC
又BF⊥AE,
所以BF⊥平面AEC
所以BF⊥AO
因为AE=AB=AC,OE=OC,
AO⊥EC
所以所以AO⊥平面BCFE
(2)因为AO⊥平面BCFE,所以AO⊥OE,AO⊥OB
又因为AE=AB,
所以0E=OB,
所以EC=BF,
又由已知四边形BCFE是菱形
所以四边形BCFE为正方形.
分析:(1)由图形及题设条件,可以先证明BF⊥AO,AO⊥EC,再由线面垂直的判定定理证明线面垂直;
(2)依据图形证明四边相等,有角为直角即可.
点评:本题考查了利用线面垂直的判定定理证明线面垂直以及正方形的定义证明四边形为正方形,是几何中的基本题型.
又BF⊥AE,
所以BF⊥平面AEC
所以BF⊥AO
因为AE=AB=AC,OE=OC,
AO⊥EC
所以所以AO⊥平面BCFE
(2)因为AO⊥平面BCFE,所以AO⊥OE,AO⊥OB
又因为AE=AB,
所以0E=OB,
所以EC=BF,
又由已知四边形BCFE是菱形
所以四边形BCFE为正方形.
分析:(1)由图形及题设条件,可以先证明BF⊥AO,AO⊥EC,再由线面垂直的判定定理证明线面垂直;
(2)依据图形证明四边相等,有角为直角即可.
点评:本题考查了利用线面垂直的判定定理证明线面垂直以及正方形的定义证明四边形为正方形,是几何中的基本题型.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 16、在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO
16、在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO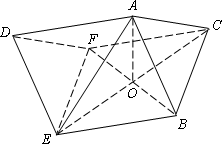
 中,已知
中,已知 ,
, ,且
,且 ,连接
,连接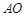 .
.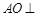 平面
平面 ;
; 为正方形.
为正方形.
