题目内容
设0<x<π,则函数![]() 的最小值是 ( )
的最小值是 ( )
A.3 B.2 C.![]() D.2-
D.2-![]()
C
解析:
解法一 因ysinx+cosx=2,故![]() .
.
由![]() ,得
,得 ![]() ,于是
,于是![]() . 因0<x<π,故y>0.又当
. 因0<x<π,故y>0.又当![]() 时,
时,![]() .若x=
.若x=![]() ,有
,有![]() ,故ymin=
,故ymin=![]() ,选C.
,选C.
解法二 由已知得:ysinx = 2 - cosx,于是y2(1-cos2x) = (2-cosx)2.
将上式整理得:(y2+1)cos2x-4cosx+4-y2=0.于是,⊿=16-4(y2+1)(4-y2)=4y2(y2-3)≥0.
因0<x<π,故y>0,于是y≥![]() ,而当y=
,而当y=![]() 时,⊿=0,cosx=
时,⊿=0,cosx=![]() ,x=
,x=![]() 满足题设,于是ymin=
满足题设,于是ymin=![]() ,选C.
,选C.
解法三 设![]() ,则
,则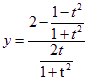
![]()
![]() ,当且仅当
,当且仅当
![]() ,即
,即![]()
![]() ,亦即x=
,亦即x=![]() 时,取“=”,故ymin=
时,取“=”,故ymin=![]() ,选C.
,选C.
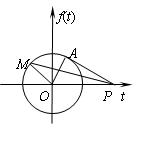
解法四 如图,单位圆中,∠MOt =![]() ,P(2,0),M(cosx,sinx),
,P(2,0),M(cosx,sinx),![]() .
.
因![]() ,故∠AOP=
,故∠AOP=![]() ,∠APt =
,∠APt =![]() ,
,
![]() ,从而,(kPM)min=
,从而,(kPM)min=![]() .
.

练习册系列答案
相关题目