题目内容
通过观察下述三个等式的规律,请你写出一个(包含下面三个命题)一般性的命题:
①sin230°+sin290°+sin2150°=
;
②sin25°+sin265°+sin2125°=
;
③sin216°+sin276°+sin2136°=
.
sin2(α+60°)+sin2(α+120°)=
=
| 3 |
| 2 |
| 3 |
| 2 |
sin2(α+60°)+sin2(α+120°)=
=
;| 3 |
| 2 |
| 3 |
| 2 |
①sin230°+sin290°+sin2150°=
| 3 |
| 2 |
②sin25°+sin265°+sin2125°=
| 3 |
| 2 |
③sin216°+sin276°+sin2136°=
| 3 |
| 2 |
分析:式子共同点是:含有三项,每项均为角的正弦的平方,三个角依次相差60°,右边结果为
.
| 3 |
| 2 |
解答:解:式子含有三项,每项均为角的正弦的平方,三个角依次相差60°,右边结果为
.
由此一般性的命题应为:sin2(α+60°)+sin2(α+120°)=
=
故答案为:sin2(α+60°)+sin2(α+120°)=
=
| 3 |
| 2 |
由此一般性的命题应为:sin2(α+60°)+sin2(α+120°)=
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:sin2(α+60°)+sin2(α+120°)=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查合情推理能力和等差数列知识,善于寻找发现规律,是此类题目的共同特点.属于基础题.

练习册系列答案
相关题目
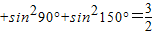 ;
;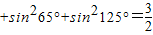 ;
; .
.