题目内容
如图，若Rt△ABC的斜边AB=2，内切圆的半径为r，则r的最大值为（ ）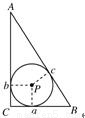
A．
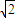
B．1
C．
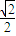
D．
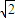-1
【答案】分析：先根据三角形内切圆的性质，用三边表示出内切圆的半径，进而根据均值不等式求得a+b的最大值，进而求的r的最大值．
解答：解：∵r=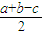
=
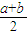-1，
∵4=a2+b2≥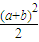
，
∴（a+b）2≤8．
∴a+b≤2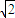
，
∴r≤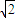
-1．
故选D．
点评：本题主要考查了基本不等式在最值问题中的应用．考查了学生运用所学知识解决实际问题的能力．
解答：解：∵r=
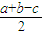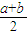=-1，∵4=a2+b2≥
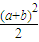，∴（a+b）2≤8．
∴a+b≤2
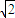，∴r≤
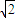-1．故选D．
点评：本题主要考查了基本不等式在最值问题中的应用．考查了学生运用所学知识解决实际问题的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
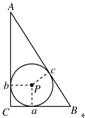如图，若Rt△ABC的斜边AB=2，内切圆的半径为r，则r的最大值为（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
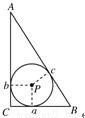
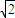
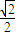
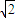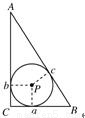
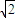
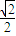
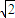-1
-1