题目内容
已知圆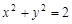 的切线l与两坐标轴分别交于点A,B两点,则
的切线l与两坐标轴分别交于点A,B两点,则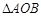 (O为坐标原点)面积的最小值为 .
(O为坐标原点)面积的最小值为 .
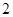
解析试题分析:因为切线l与两坐标轴分别交于点A,B两点,所以切线有斜率,并且不等于0,所以设其为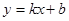 ,所以
,所以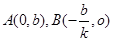 ,所以
,所以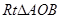 的面积等于
的面积等于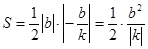 .因为直线为切线,所以
.因为直线为切线,所以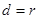 ,即
,即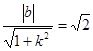 ,所以
,所以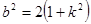 ,代入面积公式,可得
,代入面积公式,可得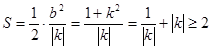 ,根据均值不等式,可知当且仅当
,根据均值不等式,可知当且仅当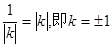 时,取得最小值.
时,取得最小值.
考点:直线与圆相切,均值不等式.

练习册系列答案
相关题目
若正数 满足
满足 ,则
,则 的最大值是( )
的最大值是( )
A. | B. | C.2 | D. |
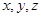 满足
满足 ,则当
,则当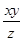 取得最大值时,
取得最大值时,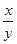 的值为 .
的值为 .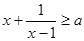 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是  的最小值为_________.
的最小值为_________.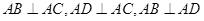 ,
,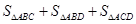 的最大值是 _______ .
的最大值是 _______ .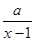 在x≥3时有最小值4,则a=_________.
在x≥3时有最小值4,则a=_________.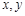 满足
满足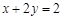 ,则
,则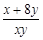 的最小值为 .
的最小值为 .