题目内容
如果对于任何实数x，不等式kx2-kx+2＞0都成立，那么实数k的取值范围是 ．
【答案】分析：对系数k分类讨论，利用“三个二次”的关系即可得出．
解答：解：①当k=0时，不等式kx2-kx+2＞0变为2＞0对任意实数x恒成立，因此k=2满足条件；
②当k≠0时，若不等式kx2-kx+2＞0对于任何实数x恒成立，则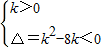
，解得0＜k＜8．
综上①②可知：实数k的取值范围是[0，8）．
故答案为[0，8）．
点评：熟练掌握分类讨论的思想方法及“三个二次”的关系是解题的关键．
解答：解：①当k=0时，不等式kx2-kx+2＞0变为2＞0对任意实数x恒成立，因此k=2满足条件；
②当k≠0时，若不等式kx2-kx+2＞0对于任何实数x恒成立，则
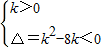，解得0＜k＜8．综上①②可知：实数k的取值范围是[0，8）．
故答案为[0，8）．
点评：熟练掌握分类讨论的思想方法及“三个二次”的关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目