题目内容
(5分)(2011•湖北)已知函数f(x)=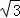 sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( )
sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( )
A.{x|kπ+ ≤x≤kπ+π,k∈Z} ≤x≤kπ+π,k∈Z} | B.{x|2kπ+ ≤x≤2kπ+π,k∈Z} ≤x≤2kπ+π,k∈Z} |
C.{x|kπ+ ≤x≤kπ+ ≤x≤kπ+ ,k∈Z} ,k∈Z} | D.{x|2kπ+ ≤x≤2kπ+ ≤x≤2kπ+ ,k∈Z} ,k∈Z} |
B
解析试题分析:利用两角差的正弦函数化简函数f(x)=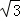 sinx﹣cosx,为一个角的一个三角函数的形式,根据f(x)≥1,求出x的范围即可.
sinx﹣cosx,为一个角的一个三角函数的形式,根据f(x)≥1,求出x的范围即可.
解:函数f(x)=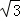 sinx﹣cosx=2sin(x﹣
sinx﹣cosx=2sin(x﹣ ),因为f(x)≥1,所以2sin(x﹣
),因为f(x)≥1,所以2sin(x﹣ )≥1,所以,
)≥1,所以,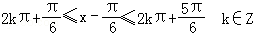
所以f(x)≥1,则x的取值范围为:{x|2kπ+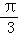 ≤x≤2kπ+π,k∈Z}
≤x≤2kπ+π,k∈Z}
故选B
点评:本题是基础题考查三角函数的化简,三角函数不等式的解法,考查计算能力,常考题型.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
函数 的图像的一个对称中心是( )
的图像的一个对称中心是( )
A. | B. | C. | D. |
已知 ,则
,则 值为( )
值为( )
A. | B.— | C.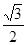 | D.—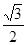 |
设角 是第二象限角,且
是第二象限角,且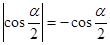 ,则
,则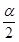 角的终边在( )
角的终边在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
将函数 的图象沿
的图象沿 轴向左平移
轴向左平移 个单位后,得到一个关于
个单位后,得到一个关于 轴对称的图象,则
轴对称的图象,则
的一个可能取值为( )
A. | B. | C. | D. |
[2014·沈阳模拟]已知tanx=2,则sin2x+1=( )
| A.0 | B. | C. | D. |
[2014·郑州调研]若函数y=2cosωx在区间[0, ]上递减,且有最小值1,则ω的值可以是( )
]上递减,且有最小值1,则ω的值可以是( )
| A.2 | B.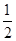 | C.3 | D.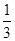 |
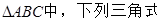 ①sin(A+B)+sinC;②cos(B+C)+cosA;③
①sin(A+B)+sinC;②cos(B+C)+cosA;③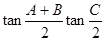
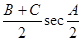 ,其中恒为定值的是 ( )
,其中恒为定值的是 ( ) )为其终边上一点,且cosα=
)为其终边上一点,且cosα= x,则x=( )
x,则x=( )