题目内容
定义在R上的函数f(x)满足f(x)= 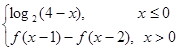 ,则f(3)的值
,则f(3)的值
为( )
| A.-1 | B.-2 | C.1 | D.2 |
B
解析

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知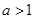 ,若函数
,若函数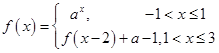 ,则
,则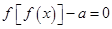 的
的
根的个数最多有
| A.1个 | B.2个 | C.3个 | D.4个 |
下列函数中,在(-1,1)内有零点且单调递增的是 ( )
A.y=log x x | B.y=2x-1 |
C.y=x2- | D.y=-x3 |
在下列四个函数中,满足性质:“对于区间(1,2)上的任意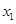 ,
,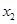 (
(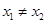 ).
). 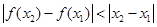 恒成立”的只有( )
恒成立”的只有( )
A.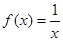 | B.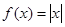 | C.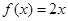 | D.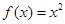 |
已知函数 是
是 上的奇函数.当
上的奇函数.当 时,
时,  ,
, 的值是( )。
的值是( )。
| A.3 | B.-3 | C.-1 | D.1 |
函数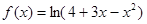 的单调递减区间是 ( )
的单调递减区间是 ( )
A.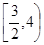 | B.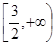 | C.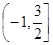 | D.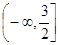 |
设f(x)是R上的奇函数,当x>0时,f(x)=2x+x,则当x<0时,f(x)=( )
A.-(- )x-x )x-x | B.-( )x+x )x+x |
| C.-2x-x | D.-2x+x |
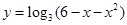 的单调减区间为( )
的单调减区间为( )
A.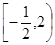 | B.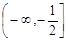 | C.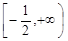 | D.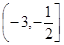 |