题目内容
设条件 p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要不充分条件,求实数a的取值范围.
分析:利用不等式的解法求解出命题p,q中的不等式范围问题,结合二者的关系得出关于字母a的不等式,从而求解出a的取值范围.
解答:解:由题意得,命题p:A={x|
≤x≤1},命题q:B={x|a≤x≤a+1},
∵?p是?q的必要不充分条件,
∴p是q的充分不必要条件,
即A⊆B,
∴a+1≥1且a≤
,
∴0≤a≤
.
故实数a的取值范围为[0,
].
| 1 |
| 2 |
∵?p是?q的必要不充分条件,
∴p是q的充分不必要条件,
即A⊆B,
∴a+1≥1且a≤
| 1 |
| 2 |
∴0≤a≤
| 1 |
| 2 |
故实数a的取值范围为[0,
| 1 |
| 2 |
点评:本题考查一元二次不等式的解法,考查二次不等式与二次函数的关系,注意等价转化思想的运用.

练习册系列答案
相关题目
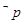 是
是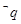 的必要不充分条件,求实数a的去值范围.
的必要不充分条件,求实数a的去值范围.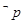 是
是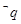 的必要不充分条件,求实数a的去值范围.
的必要不充分条件,求实数a的去值范围.