题目内容

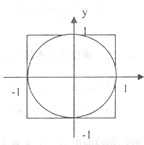
 在正方形中随机撒一把豆子,通过考察落在其内切圆内黄豆的数目,用随机模拟的方法可计算圆周率P的近似值(如图)
在正方形中随机撒一把豆子,通过考察落在其内切圆内黄豆的数目,用随机模拟的方法可计算圆周率P的近似值(如图)(1)用两个均匀随机数x,y构成的一个点的坐标(x,y)代替一颗豆子,请写出随机模拟法的方案;
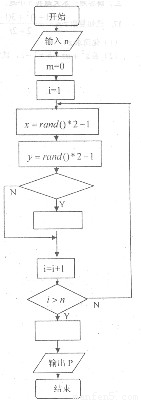
(2)以下程序框图用以实现该模拟过程,请将它补充完整.(注:rand是计算机在Excel中产生[0,1)区间上的均匀随机数的函数)
分析:用随机模拟的方法可以估算点落在圆内的概率,由几何概率公式可得点落在圆内的概率为,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值
解答:解:(1)具体方案如下
①利用计算机产生两组[0,1]上的均匀随机数,x=RAND,y=RAND;
②统计试验总次数N和落在阴影内的点数N1(满足条件x2+y2≤1的点(x,y)的个数);
③计算频率
,即为点落在圆内的概率的近似值;
④设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=
.
∴
=
.
∴S≈
,即为圆的面积的近似值.
又S圆=πr2=π,∴π=S≈
,即为圆周率的近似值.
(2)由题意
第一个判断框中应填x2+y2≤1
其下的处理框中应填m=m+1
退出循环体后的处理框中应填P=
①利用计算机产生两组[0,1]上的均匀随机数,x=RAND,y=RAND;
②统计试验总次数N和落在阴影内的点数N1(满足条件x2+y2≤1的点(x,y)的个数);
③计算频率
| N1 |
| N |
④设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=
| S |
| 4 |
∴
| S |
| 4 |
| N1 |
| N |
∴S≈
| 4N1 |
| N |
又S圆=πr2=π,∴π=S≈
| 4N1 |
| N |
(2)由题意
第一个判断框中应填x2+y2≤1
其下的处理框中应填m=m+1
退出循环体后的处理框中应填P=
| m |
| n |
点评:本题考查模拟方法估计概率,解题的关键是理解模拟方法求概率的原理及随机数产生的原理,本题是模拟方法求概率的应用,这是现代数学求圆周率常用的方法,利用现代高科技求解数学问题.

练习册系列答案
相关题目
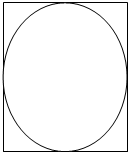 如图,在正方形中随机撒一把豆子,用随机模拟的方法估算圆周率π的值.正方形的边长2,若总豆子数n=1000,其中落在圆内的豆子数m=790,则估算圆周率π的值是
如图,在正方形中随机撒一把豆子,用随机模拟的方法估算圆周率π的值.正方形的边长2,若总豆子数n=1000,其中落在圆内的豆子数m=790,则估算圆周率π的值是 如图,在正方形中随机撒一把豆子,用随机模拟的方法估算圆周率π的值.正方形的边长2,若总豆子数n=1000,其中落在圆内的豆子数m=790,则估算圆周率π的值是________.
如图,在正方形中随机撒一把豆子,用随机模拟的方法估算圆周率π的值.正方形的边长2,若总豆子数n=1000,其中落在圆内的豆子数m=790,则估算圆周率π的值是________.