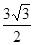题目内容
如果函数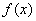 对于区间D内任意的
对于区间D内任意的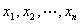 ,有
,有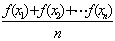
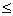
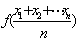 成立,称
成立,称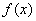 是区间D上的“凸函数”.已知函数
是区间D上的“凸函数”.已知函数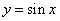 在区间
在区间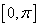 上是 “凸函数”,则在△
上是 “凸函数”,则在△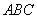 中,
中,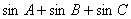 的最大值是( )
的最大值是( )
A.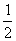 B.
B.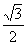 C.
C.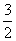 D.
D.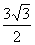
【答案】
D
【解析】
试题分析:利用“凸函数”的定义得到恒成立的不等式,利用三角形的内角和为π,求出函数的最大值.解:∵y=sinx在区间[0,π]上是“凸函数”,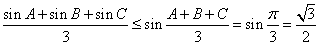 可知
可知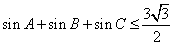 ,故选D.
,故选D.
考点:新定义的运用
点评:本题考查理解题中的新定义、并利用新定义求最值、考查三角形的内角和为π.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
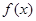 对于区间D内任意的
对于区间D内任意的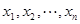 ,有
,有
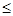
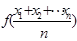 成立,称
成立,称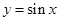 在区间
在区间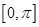 上是“凸函数”,则在△
上是“凸函数”,则在△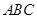 中,
中,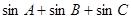 的最大值是( )
的最大值是( )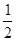 (B)
(B)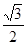 (C)
(C)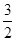 (D)
(D)