题目内容
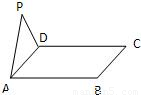
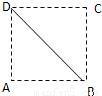
如图所示，△ADP为正三角形，四边形ABCD为正方形，平面PAD⊥平面ABCD、点M为平面ABCD内的一个动点，且满足MP=MC、则点M在正方形ABCD内的轨迹为（ ）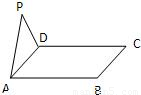
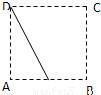
A．
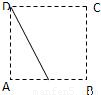
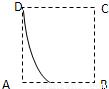
B．
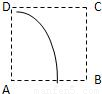
C．
D．
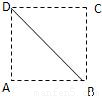
【答案】分析：在空间中，过线段PC中点，且垂直线段PC的平面上的点到P，C两点的距离相等，此平面与平面ABCD相交，两平面有一条公共直线．
解答：解：在空间中，存在过线段PC中点且垂直线段PC的平面，平面上点到P，C两点的距离相等，记此平面为α
平面α与平面ABCD有一个公共点，则它们有且只有一条过该点的公共直线．
故选A．
点评：本题是轨迹问题与空间线面关系相结合的题目，有助于学生提高学生的空间想象能力．
解答：解：在空间中，存在过线段PC中点且垂直线段PC的平面，平面上点到P，C两点的距离相等，记此平面为α
平面α与平面ABCD有一个公共点，则它们有且只有一条过该点的公共直线．
故选A．
点评：本题是轨迹问题与空间线面关系相结合的题目，有助于学生提高学生的空间想象能力．
练习册系列答案
相关题目
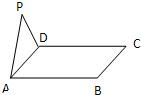8、如图所示，△ADP为正三角形，四边形ABCD为正方形，平面PAD⊥平面ABCD、点M为平面ABCD内的一个动点，且满足MP=MC、则点M在正方形ABCD内的轨迹为（ ）
